已知 分别是椭圆
分别是椭圆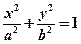
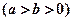 的左、右 焦点,已知
的左、右 焦点,已知
点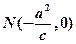 满足
满足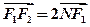 ,且
,且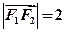 。设
。设 是上半椭圆上且满足
是上半椭圆上且满足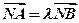 的两点。
的两点。
(1)求此椭圆的方程;
(2)若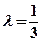 ,求直线AB的斜率。
,求直线AB的斜率。
设函数f(x)=|2x-1|+|2x-3|,x∈R
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若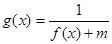 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
已知曲线C的极坐标方程为 ,直线
,直线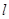 的参数方程为
的参数方程为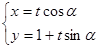 ( t为参数,0≤
( t为参数,0≤ <
<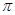 ).
).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线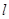 经过点(1,0),求直线
经过点(1,0),求直线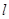 被曲线C截得的线段AB的长.
被曲线C截得的线段AB的长.
已知函数 .
.
(Ⅰ)求函数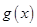 的单调区间;
的单调区间;
(Ⅱ)若函数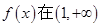 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;
(Ⅲ)若 ,使
,使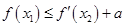 (
(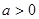 )成立,求实数a的取值范围.
)成立,求实数a的取值范围.
已知两点 及
及 ,点
,点 在以
在以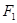 、
、 为焦点的椭圆
为焦点的椭圆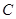 上,且
上,且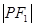 、
、 、
、 构成等差数列.
构成等差数列.
(Ⅰ)求椭圆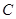 的方程;
的方程;
(Ⅱ)如图,动直线 与椭圆
与椭圆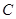 有且仅有一个公共点,点
有且仅有一个公共点,点 是直线
是直线 上的两点,且
上的两点,且 ,
, . 求四边形
. 求四边形 面积
面积 的最大值.
的最大值.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD丄CD,AB//CD,AB=AD= CD=2,点M在线段EC上.
CD=2,点M在线段EC上.
(I)当点M为EC中点时,求证: 面
面 ;
;
(II)求证:平面BDE丄平面BEC;
(III)若平面说BDM与平面ABF所成二面角锐角,且该二面角的余弦值为 时,求三棱锥M-BDE的体积.
时,求三棱锥M-BDE的体积.