(本小题满分14分)已知在平面直角坐标系xoy中的一个椭圆,它的中心在原
点,左焦
(1)求该椭圆的标准方程;
(2)若P是椭圆上的动点,求线段PA中点M的轨迹方程;
(3)过原点O的直线交椭圆于点B、C,求△ABC面积的最大值。
如图,已知三棱锥 的侧棱
的侧棱 两两垂直,且
两两垂直,且 ,
, ,
, 是
是 的中点。
的中点。
(1)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)求 和平面
和平面 所成角的正弦值。
所成角的正弦值。
用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
已知函数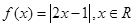 ,
,
(1)解不等式 ;
;
(2)若对于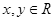 ,有
,有 .求证:
.求证: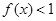 .
.
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为
(t为参数),再以原点为极点,以x正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为 .
.
(1)求圆C的直角坐标方程;
(2)设圆C与直线 将于点
将于点 、
、 ,若点
,若点 的坐标为
的坐标为 ,求
,求 的值 .
的值 .
如图,圆 与圆
与圆 内切于点
内切于点 ,其半径分别为3与2,圆
,其半径分别为3与2,圆 的弦
的弦 交圆
交圆 于点
于点 (
( 不在
不在 上),
上), 是圆
是圆 的一条直径.
的一条直径.
(1)求 的值;
的值;
(2)若 ,求
,求 到弦
到弦 的距离.
的距离.