已知点 ,
, 是平面内一动点,直线
是平面内一动点,直线 、
、 斜率之积为
斜率之积为 。
。
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 作直线
作直线 与轨迹
与轨迹 交于
交于 两点,线段
两点,线段 的中点为
的中点为 ,求直线
,求直线 的斜率
的斜率 的取值范围。
的取值范围。
如图,圆 内有一点P(—1,2),AB为过点P的弦。
内有一点P(—1,2),AB为过点P的弦。
(1)当弦AB的倾斜角为135°时,求AB所在的直线方程及|AB|;
(2)当弦AB被点P平分时,写出直线AB的方程。
如图,在长方体 中,点
中,点 在棱
在棱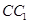 的延长线上,且
的延长线上,且 .
.
(Ⅰ)求证: //平面
//平面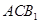 ;
;
(Ⅱ)求证:平面
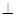 平面
平面 ;
;
【改编】已知圆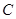 :
:
(1)平面上有两点 ,求过点
,求过点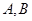 两点的直线
两点的直线 被圆
被圆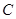 截得的弦长;
截得的弦长;
(2)已知过点 的直线
的直线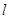 平分圆
平分圆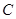 的周长,
的周长, 是直线
是直线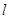 上的动点,求
上的动点,求 的最大值.
的最大值.
(3) 若 是
是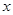 轴上的动点,
轴上的动点,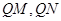 分别切圆
分别切圆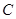 于
于 两点.
两点.
试问:直线 是否恒过定点?如是,求出定点坐标,如不是,说明理由.
是否恒过定点?如是,求出定点坐标,如不是,说明理由.
【原创】如图:直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分别是边AD和BC上的点,且EF∥AB,AD ="2AE" ="2AB" =" 4CF=" 4,将四边形EFCD沿EF折起使AE=AD.
(1)求证:AF∥平面CBD;
(2)求几何体ADE-BCF的体积.
已知:矩形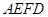 的两条对角线相交于点
的两条对角线相交于点 ,
,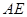 边所在直线的方程为:
边所在直线的方程为:  ,点
,点 在
在 边所在直线上.
边所在直线上.
(1)求矩形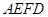 外接圆
外接圆 的方程。
的方程。
(2) 是圆
是圆 的内接三角形,其重心
的内接三角形,其重心 的坐标是
的坐标是 ,求直线
,求直线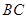 的方程 .
的方程 .