设函数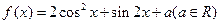 .
.
(1)求函数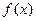 的最小正周期.
的最小正周期.
(2)当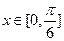 时,
时,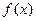 的最大值为2,求
的最大值为2,求 的值,
的值,
如图所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的,
分别为
的中点,
分别为
,
的中点.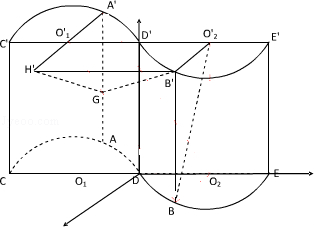
(1)证明:
四点共面;
(2)设
为
中点,延长
到
,使得
.证明:
平面
.
在某次测验中,有6位同学的平均成绩为75分.用
表示编号为
(
=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号 | 1 |
2 |
3 |
4 |
5 |
| 成绩
|
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩
,及这6位同学成绩的标准差
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
已知函数
.
(1)求
的值;
(2)设
.求
的值.
已知
为常数,且
,函数
,
(
=2.71828…是自然对数的底数).
(I)求实数
的值;
(II)求函数
的单调区间;
(III)当
=1时,是否同时存在实数
和
(
),使得对每一个
,直线
与曲线
都有公共点?若存在,求出最小的实数
和最大的实数
;若不存在,说明理由.
设函数
,其中,角
的顶点与坐标原点重合,始边与
轴非负半轴重合,终边经过点
,且
.
(Ⅰ)若点
的坐标为
,求
的值;
(Ⅱ)若点
为平面区域
上的一个动点,试确定角
的取值范围,并求函数
的最小值和最大值.