如图所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的,
分别为
的中点,
分别为
,
的中点.
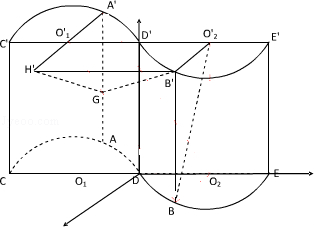
(1)证明:
四点共面;
(2)设
为
中点,延长
到
,使得
.证明:
平面
.
解关于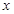 的不等式
的不等式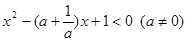
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量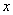 (吨)与相应的生产能耗
(吨)与相应的生产能耗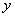 (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
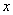 |
3 |
4 |
5 |
6 |
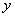 |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出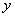 关于
关于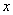 的线性回归方程;
的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值: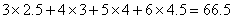 )
)
已知向量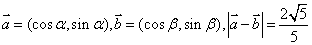
(1)求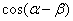 的值
的值
(2)若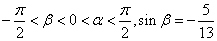 ,求
,求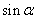 的值.
的值.
已知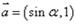 ,
,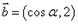 ,
,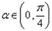 .
.
(1)若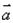 ∥
∥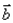 ,求
,求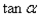 的值;
的值;
(2)若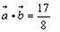 ,求
,求
一个口袋内装有大小相同的5 个球,其中3个白球分别记为:A1、A2、A3;2个黑球分别记为B1、B2,从中一次摸出2个球.(Ⅰ)写出所有的基本事件;(Ⅱ)求摸出2球均为白球的概率.