椭圆C: 长轴为8离心率
长轴为8离心率
(1)求椭圆C的标准方程;
(2)过椭圆C内一点M(2,1)引一条弦,使弦被点M平分,
求这条弦所在的直线方程。
设 是不共线的向量,已知向量
是不共线的向量,已知向量 ,若A,B,D三点共线,求k的值
,若A,B,D三点共线,求k的值
已知函数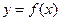 是定义域为R的偶函数,其图像均在x轴的上方,对任意的
是定义域为R的偶函数,其图像均在x轴的上方,对任意的 ,都有
,都有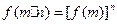 ,且
,且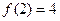 ,又当
,又当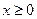 时,其导函数
时,其导函数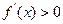 恒成立。
恒成立。
(Ⅰ)求 的值;
的值;
(Ⅱ)解关于x的不等式: ,其中
,其中
设x1、x2、y1、y2是实数,且满足x12+x22≤1,
证明不等式(x1y1+x2y2-1)2≥(x12+x22-1)(y12+y22-1).
5.12四川汶川大地震,牵动了全国各地人民的心,为了安置广 大灾民,抗震救灾指挥部决定建造一批简易房(每套长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造,每平方米材料费为200元.每套房材料费控制在32000元以内,试计算:
大灾民,抗震救灾指挥部决定建造一批简易房(每套长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造,每平方米材料费为200元.每套房材料费控制在32000元以内,试计算:
(1)设房前面墙的长为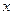 ,两侧墙的长为
,两侧墙的长为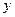 ,所用材料费为
,所用材料费为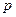 ,试用
,试用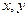 表示
表示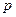 ;
;
(2)求简易房面积S的最大值是多少?并求S最大时,前面墙的长度应设计为多少米?
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表所:
| 类型 |
A规格 |
B规格 |
C规格 |
| 第一种钢板 |
1 |
2 |
1 |
| 第二种钢板 |
1 |
1 |
3 |
每张钢板的面积:第一种为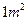 ,第二种为
,第二种为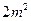 。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?