（本小题满分8分）2011年6月4日，李娜获得法网公开赛的冠军，圆了中国人
的网球梦，也在国内掀起一股网球热。某市准备为青少年举行一次网球知识讲座，小明和妹
妹都是网球球迷，要求爸爸去买门票，但爸爸只买回一张门票，那么谁去就成了问题，小明
想到一个办法：他拿出一个装有质地、大小相同的
个红球与
个白球的袋子，让爸爸摸
出一个球，如果摸出的是红球，妹妹去听讲座，如果摸出的是白球，小明去听讲座。
（1）爸爸说这个办法不公平，请你用概率的知识解释原因。
（2）若爸爸从袋中取出
个白球，再用小明提出的办法来确定谁去听讲座，请问摸球的结果是对小明有利还是对妹妹有利，说明理由。
如图，两直线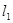
：
、
：
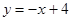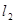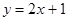相交于点P，与
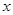轴分别相交于A、B两点．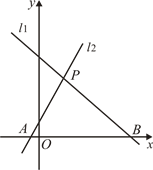
（1）求P点的坐标；
（2）求S△PAB．
“最美女教师”张丽莉，为抢救两名学生，以致双腿高位截肢，社会各界纷纷为她捐款，我市某中学九年级一班全体同学参加了捐款活动，该班同学捐款情况的部分统计图如图所示：
（1）求该班的总人数；
（2）将条形图补充完整，并写出捐款总额的众数；
（3）该班平均每人捐款多少元？
如图，图中的小方格都是边长为1的正方形，
的顶点坐标分别为
，
，
．
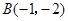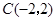（1）请在图中画出绕
点顺时针旋转
后的图形；
（2）请直接写出以
为顶点的平行四边形的第四个顶点
的坐标．
计算：
－
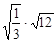
某宾馆客房有三人客房、双人客房，收费数据如下表：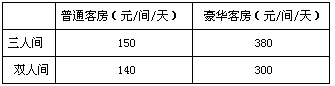
为吸引游客，实行团体入住五折优惠措施，一个50人的旅游团优惠期间到该宾馆入住，住了若干间三人普通间客房和双人普通房间客房。若每间客房正好住满，且一天共花去住宿费1510元，则旅游团住了三人普通间和双人普通间客房各多少间？