阅读下面材料：
小明遇到这样一个问题：如图1，在边长为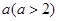
的正方形ABCD各边上分别截取AE＝BF＝CG＝DH＝1，当∠AFQ＝∠BGM＝∠CHN＝∠DEP＝45°时，求正方形MNPQ的面积．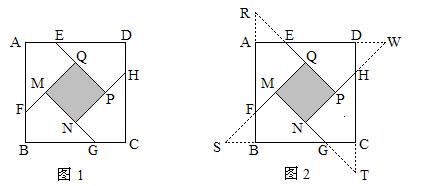
小明发现：分别延长QE，MF， NG，PH，交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）。请回答：
（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙，不重叠），则这个新的正方形的边长为__________；
（2）求正方形MNPQ的面积．
（3）参考小明思考问题的方法，解决问题：
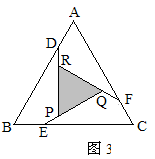
如图3，在等边△ABC各边上分别截取AD＝BE＝CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ，若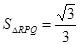
，则AD的长为__________．
2013年2月28日，全国科学技术名词审定委员会称PM2．5拟正式命名为“细颗粒物”。 PM2．5值越大，空气污染越严重。小敏为了解本市的空气质量情况，从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．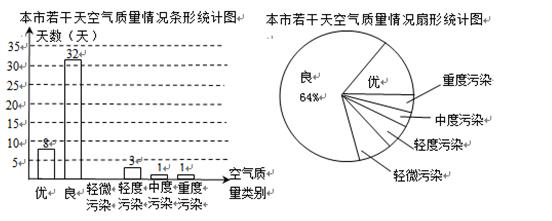
请你根据图中提供的信息，解答下列问题：
（1）本次共抽取了天；
（2）请补全条形统计图，扇形统计图中表示优的扇形的圆心角度数为°；
（3）请估计该市这一年（365天）达到优和良的总天数．
（1）解方程：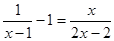
；
（2）解不等式：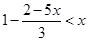
，并把解集表示在数轴上．
（1）计算：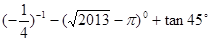
；
（2）化简：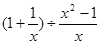
．
如图，∠C=90°，点A、B在∠C的两边上，CA=30，CB=20，连结AB．点
P从点B出发，以每秒4个单位长度的速度沿BC方向运动，到点C停止．当点P与B、C两点不重合时，作PD⊥BC交AB于D，作DE⊥AC于E．F为射线CB上一点，且∠CEF=∠ABC．设点P的运动时间为x（秒）．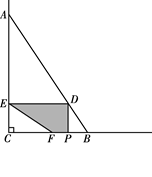
（1）用含有x的代数式表示CE的长；
（2）求点F与点B重合时x的值；
（3）当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y（平方单位）．求y与x之间的函数关系式；
（4）当x为某个值时，沿PD将以D、E、F、B为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的x值．
如图1，抛物线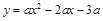
（
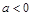），与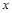
轴的交于A、B两点（点
A在点B的右侧），与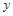
轴的正半轴交于点C，顶点为D．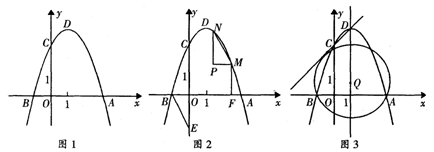
（1）求顶点D的坐标（用含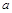
的代数式表示）；
（2）若以AD为直径的圆经过点C．
① 求抛物线的解析式；
② 如图2，点E是y轴负半轴上的一点，连结BE，将△OBE绕平面内某一点旋转180°，得到△PMN（点P、M、N分别和点O、B、E对应），并且点M、N都在抛物线上，作MF⊥x轴于点F，若线段MF：BF=1：2，求点M、N的坐标；
③ 点Q在抛物线的对称轴上，以Q为圆心的圆过A、B两点，并且和直线CD相切，如图3，求点Q的坐标．