如图1,抛物线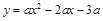 (
(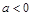 ),与
),与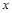 轴的交于A、B两点(点
轴的交于A、B两点(点
A在点B的右侧),与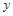 轴的正半轴交于点C,顶点为D.
轴的正半轴交于点C,顶点为D.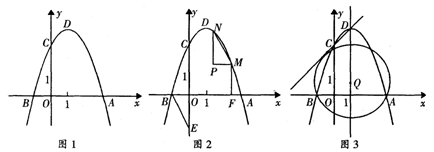
(1)求顶点D的坐标(用含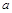 的代数式表示);
的代数式表示);
(2)若以AD为直径的圆经过点C.
① 求抛物线的解析式;
② 如图2,点E是y轴负半轴上的一点,连结BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③ 点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.
小华初中就要毕业了,她就本班同学的升学志愿进行了一次调查统计,她通过采集数据后,绘制了两幅不完整的统计图.请你根据图中提供的信息,解答下列问题:

(1)求出该班的总人数;
(2)通过计算请把图(1)统计图补充完整;
(3)如果小华所在年级共有600名学生,请你估计该年级报考普高的学生有多少人.
如图,图1和图2都是7×4正方形网格,每个小正方形的边长为l,请按要求画出下列图形,所画图形的各个顶点均在所给小正方形的顶点上.
(1)在图1中画出一个等腰直角三角形ABC;
(2)在图2中画出一个钝角三角形ABD,使△ABD的面为3.
先化简,再求值: ,其中a=tan60°+2.
,其中a=tan60°+2.
市交警支队对某校学生进行交通安全知识宣传,事先以无记名的方式随机调查了该校部分学生闯红灯的情况,并绘制成如图所示的统计图.请根据图中的信息回答下列问题: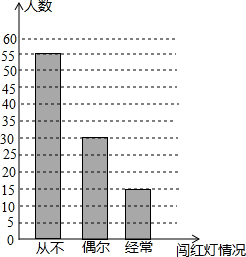
(1)本次共调查了多少名学生?
(2)如果该校共有1500名学生,请你估计该校经常闯红灯的学生大约有多少人;
(3)针对图中反映的信息谈谈你的认识.(不超过30个字)
(1)先求解下列两题:
①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数 (x>0)的图象经过点B,D,求k的值.
(x>0)的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出.