如图,∠C=90°,点A、B在∠C的两边上,CA=30,CB=20,连结AB.点
P从点B出发,以每秒4个单位长度的速度沿BC方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于D,作DE⊥AC于E.F为射线CB上一点,且∠CEF=∠ABC.设点P的运动时间为x(秒).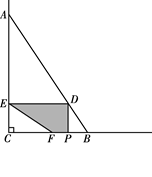
(1)用含有x的代数式表示CE的长;
(2)求点F与点B重合时x的值;
(3)当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式;
(4)当x为某个值时,沿PD将以D、E、F、B为顶点的四边形剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的x值.
无论k取任何实数,对于直线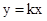 都会经过一个固定的点
都会经过一个固定的点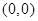 ,我们就称直线
,我们就称直线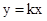 恒过定点
恒过定点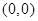 .
.
(1)无论 取任何实数,抛物线
取任何实数,抛物线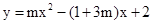 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点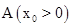 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线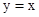 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为 . 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
. 在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.
(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;
(2)当点C在直线BE上时,连接FC,直接写出∠FCD 的度数;
(3)如图3,如果 =45°,AB =2,AE=
=45°,AB =2,AE=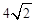 ,求点G到BE的距离.
,求点G到BE的距离.
如图,已知二次函数 (a≠0)的图象经过点A,点B.
(a≠0)的图象经过点A,点B.
(1)求二次函数的表达式;
(2)若反比例函数 (x>0)的图象与二次函数
(x>0)的图象与二次函数 (a≠0)的图象在第一象限内交于点
(a≠0)的图象在第一象限内交于点 ,
, 落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数;
落在两个相邻的正整数之间,请你直接写出这两个相邻的正整数;
(3)若反比例函数 (x>0,k>0)的图象与二次函数
(x>0,k>0)的图象与二次函数 (a≠0)的图象在第一象限内交于点
(a≠0)的图象在第一象限内交于点 ,且
,且 ,试求实数k的取值范围.
,试求实数k的取值范围.
图1是李晨在一次课外活动中所做的问题研究:他用硬纸片做了两个三角形,分别为△ABC和△DEF,其中∠B=90°,∠A=45°,BC= ,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
(1)请回答李晨的问题:若CD=10,则AD=;
(2)如图2,李晨同学连接FC,编制了如下问题,请你回答:
①∠FCD的最大度数为;
②当FC∥AB时,AD=;
③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形,且FC为斜边时,AD=;
④△FCD的面积s的取值范围是.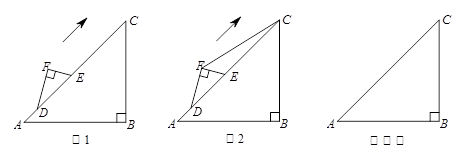
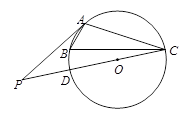
如图,已知A、B、C分别是⊙O上的点,∠B=60°,P是直径CD的延长线上的一点,且AP=AC.
(1)求证:AP与⊙O相切;
(2)如果AC=3,求PD的长.