直线y=―x―2与反比例函数y=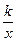
的图像交于Ａ、Ｂ两点，且与x、y轴交于C、D两点，A点的坐标为（－3，k＋4）.
（1）求反比例函数的解析式
（2）把直线AB绕着点M（―1，―1）顺时针旋转到MN，使直线MN⊥x轴，且与反比例函数的图像交于点N，求旋转角大小及线段MN的长。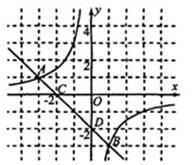
如图，四边形ABCD是菱形，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F，连接CE．
（1）求证：∠DAE＝∠DCE；
（2）当AE＝2EF时，判断FG与EF有何等量关系？并证明你的结论？
已知：如图一次函数y＝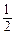
x＋1的图象与x轴交于点A，与y轴交于点B；二次函数y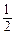＝x2＋bx＋c的图象与一次函数y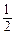＝x＋1的图象交于B、C两点，与x轴交于D、E两点且D点坐标为(1，0)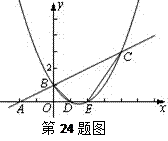
(1)求二次函数的解析式；
(2)求四边形BDEC的面积S；
(3)在x轴上是否存在点P，使得△PBC是以P为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由．
为了抓住世博会商机，某商店决定购进A、B两种世博会纪念品．若购进A种纪念品10件，B种纪念品5件，需要1000元；若购进A种纪念品5件，B种纪念品3件，需要550元．
（1）求购进A、B两种纪念品每件各需多少元？
（2）若该商店决定拿出1万元全部用来购进这两种纪念品，考虑市场需求，要求购进A种纪念品的数量不少于B种纪念品数量的6倍，且不超过B种纪念品数量的8倍，那么该商店共有几种进货方案？
（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？
关于x的方程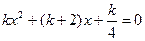
有两个不相等的实数根.
(1)求k的取值范围。
(2)是否存在实数k，使方程的两个实数根的倒数和等于0?若存在，求出k的值；若不存在，说明理由
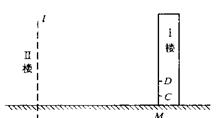
如图所示，某居民楼Ⅰ高20米，窗户朝南。该楼内一楼住户的窗台离地面距离CM为2米，窗户CD高1.8米。现计划在I楼的正南方距I楼30米处新建一居民楼Ⅱ。当正午时刻太阳光线与地面成30°角时，要使Ⅱ楼的影子不影响I楼所有住户的采光，新建Ⅱ楼最高只能盖多少米?