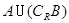如图,以原点O为顶点,以y轴为对称轴的抛物线E的焦点为F(0,1),点M是直线l:y=m(m<0)上任意一点,过点M引抛物线E的两条切线分别交x轴于点S,T,切点分别为B,A.
(I)求抛物线E的方程;
(Ⅱ)求证:点S,T在以FM为直径的圆上;
(Ⅲ)当点M在直线l上移动时,直线AB恒过焦点F,求m的值.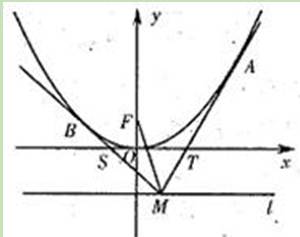
(本小题满分14分)某商品在近30天内,每件的销售价格P(元)与时间t(天)的函数关系是:
该商品的日销售量Q(件)与时间(天)的函数关系是:Q=-t+40 (0<t≤30,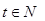 ),
),
求:这种商品日销售金额y(元)的最大值,并指出日销售金额最大的一天是30天中的哪一天?
(本小题满分14分)已知函数函数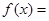

(1)判断并证明函数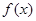 的奇偶性;
的奇偶性;
(2)证明函数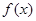 在
在 上是增函数。
上是增函数。
(3)若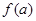 >2,求
>2,求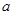 的取值范围。
的取值范围。
(本小题满分14分)已知二次函数 ,且满足
,且满足
(1)求函数 的表达式;
的表达式;
(2)设函数 ,若
,若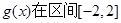 上是单调函数,求实数
上是单调函数,求实数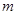 的取值范围。
的取值范围。
(本小题满分12分)
(1)若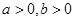 ,化简:
,化简:
(2)若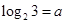 ,
,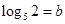 ,试用
,试用 表示
表示
(本小题满分12分)设A=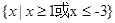 ,B=
,B= 求:
求:
(1)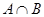 ,
,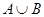
(2)