(本小题满分14分)某商品在近30天内,每件的销售价格P(元)与时间t(天)的函数关系是:
该商品的日销售量Q(件)与时间(天)的函数关系是:Q=-t+40 (0<t≤30,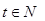 ),
),
求:这种商品日销售金额y(元)的最大值,并指出日销售金额最大的一天是30天中的哪一天?
(本小题满分12分)已知命题 实数
实数 满足
满足 ,命题
,命题 实数
实数 满足
满足
 ,若
,若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知关于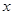 的不等式
的不等式 的解集为
的解集为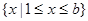 .
.
(1)求实数 的值;
的值;
(2)解关于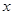 的不等式:
的不等式: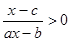 (
( 为常数).
为常数).
(本小题满分10分)已知 的内角
的内角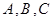 所对边分别为
所对边分别为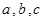 ,且
,且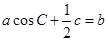 .
.
(1)求角 的大小;
的大小;
(2)若 ,求边长
,求边长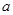 的最小值.
的最小值.
(本小题满分12分)已知椭圆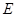 的两个焦点分别为
的两个焦点分别为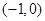 和
和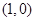 ,离心率
,离心率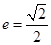 .
.
(1)求椭圆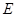 的方程;
的方程;
(2)设直线 (
(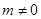 )与椭圆
)与椭圆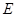 交于
交于 、
、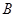 两点,线段
两点,线段 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,当
,当 变化时,求
变化时,求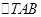 面积的最大值.
面积的最大值.
(本小题满分12分)已知中心在原点的椭圆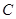 的左焦点
的左焦点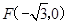 ,右顶点
,右顶点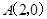 .
.
(1)求椭圆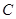 的标准方程;
的标准方程;
(2)斜率为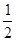 的直线
的直线 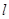 与椭圆
与椭圆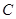 交于
交于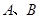 两点,求弦长
两点,求弦长 的最大值及此时
的最大值及此时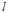 的直线方程.
的直线方程.