(本小题满分12分)已知椭圆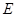 的两个焦点分别为
的两个焦点分别为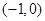 和
和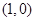 ,离心率
,离心率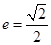 .
.
(1)求椭圆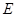 的方程;
的方程;
(2)设直线 (
(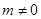 )与椭圆
)与椭圆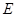 交于
交于 、
、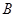 两点,线段
两点,线段 的垂直平分线交
的垂直平分线交 轴于点
轴于点 ,当
,当 变化时,求
变化时,求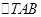 面积的最大值.
面积的最大值.
已知命题p: x∈[1,2],x2-a≥0;命题q:
x∈[1,2],x2-a≥0;命题q: x0∈R,使得x+(a-1)x0+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围。
x0∈R,使得x+(a-1)x0+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围。
已知函数 ,
, .
.
(1)若对任意的实数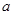 ,函数
,函数 与
与 的图象在
的图象在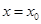 处的切线斜率总相等,求
处的切线斜率总相等,求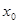 的值;
的值;
(2)若 ,对任意
,对任意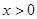 ,不等式
,不等式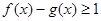 恒成立,求实数
恒成立,求实数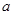 的取值范围.
的取值范围.
如图,直四棱柱ABCD–A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=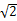 ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3
(1)证明:BE⊥平面BB1C1C;
(2)求点 到平面EA1C1的距离.
到平面EA1C1的距离.
在 中,角
中,角 所对的边分别为
所对的边分别为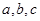 ,且满足
,且满足
(1)若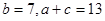 ,求
,求 的面积;
的面积;
(2)求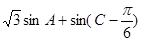 的取值范围.
的取值范围.
已知p:f(x)= ,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
,且|f(a)|<2;q:集合A={x|x2+(a+2)x+1=0,x∈R},且A≠Ø.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.