.( 本小题满分12分)
本小题满分12分)
在直角坐标系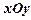 中,椭圆
中,椭圆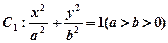 的左、右焦点分别为
的左、右焦点分别为 . 其中
. 其中 也是抛物线
也是抛物线 的焦点,点
的焦点,点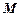 为
为 与
与 在第一象限的交点,且
在第一象限的交点,且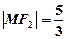
(Ⅰ)求 的方程;
的方程;
(Ⅱ)若过点 的直线
的直线 与
与 交于不同的两点
交于不同的两点 .
.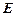 在
在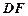 之间,试求
之间,试求 与
与 面积之比的取值范围.(O为坐标原点)
面积之比的取值范围.(O为坐标原点)
设 R,函数
R,函数 .
.
(1)若x=2是函数y=f(x)的极值点,求实数a的值;
(2)若函数 在区间[0,2]上是减函数,求实数a的取值范围.
在区间[0,2]上是减函数,求实数a的取值范围.
如图,矩形ABCD中,|AB|=4,|BC|=2,E,F,M,N分别是矩形四条边的中点,G,H分别是线段ON,CN的中点.
(1)证明:直线EG与FH的交点L在椭圆W: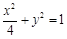 上;
上;
(2)设直线l: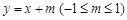 与椭圆W:
与椭圆W: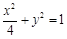 有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求
有两个不同的交点P,Q,直线l与矩形ABCD有两个不同的交点S,T,求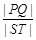 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.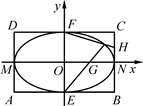
已知抛物线的方程为 ,直线l过定点
,直线l过定点 ,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?
函数 .
.
(1)求函数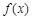 的极值;
的极值;
(2)设函数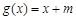 ,对
,对 ,都有
,都有 ,求实数m的取值范围.
,求实数m的取值范围.
设命题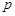 :函数y=kx+1在R上是增函数,命题
:函数y=kx+1在R上是增函数,命题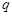 :曲线
:曲线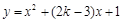 与x轴交于不同的两点,如果
与x轴交于不同的两点,如果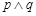 是假命题,
是假命题,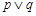 是真命题,求k的取值范围.
是真命题,求k的取值范围.