(本小题满分12分)
已知函数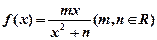 在
在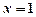 处取到极值2
处取到极值2
(Ⅰ)求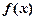 的解析式;
的解析式;
(Ⅱ)设函数 .若对任意的
.若对任意的 ,总存在唯一的
,总存在唯一的 ,使得
,使得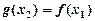 ,求实数
,求实数 的取值范围.
的取值范围.
如图,在直三棱柱 中, 已知
中, 已知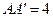 ,
,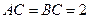 ,
,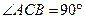 ,
, 是
是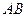 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求直线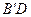 与平面
与平面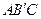 所成角的正弦值.
所成角的正弦值.
 |
(本小题满分14分)已知数列 的前
的前 项和为
项和为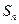 ,
, ,
,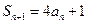 ,设
,设 .
.
(Ⅰ)证明数列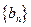 是等比数列;
是等比数列;
(Ⅱ)数列 满足
满足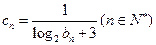 ,设
,设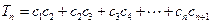 ,若对一切
,若对一切 不等式
不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)函数 ,其中
,其中 ,若存在实数
,若存在实数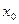 ,使得
,使得 成立,则称
成立,则称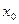 为
为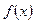 的不动点.
的不动点.
(1)当 ,
, 时,求
时,求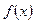 的不动点;
的不动点;
(2)若对于任何实数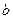 ,函数
,函数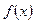 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数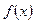 的图像上
的图像上 两点的横坐标是函数
两点的横坐标是函数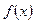 的不动点,且直线
的不动点,且直线 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数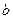 的取值范围.
的取值范围.
(本小题满分14分)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。
(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求点C到平面A1BD的距离.
(本小题满分14分)如图,一架直升飞机的航线和山顶在同一个垂直于地面的平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞行员先看到山顶的俯角为 ,经过2分钟后又看到山顶的俯角为
,经过2分钟后又看到山顶的俯角为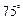 ,求山顶的海拔高度.
,求山顶的海拔高度. 