(本小题满分14分)已知数列 的前
的前 项和为
项和为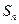 ,
, ,
,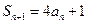 ,设
,设 .
.
(Ⅰ)证明数列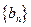 是等比数列;
是等比数列;
(Ⅱ)数列 满足
满足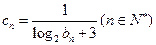 ,设
,设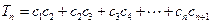 ,若对一切
,若对一切 不等式
不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
定义:若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”。已知数列
为“平方递推数列”。已知数列 中,
中, ,点
,点 在函数
在函数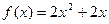 的图像上,其中
的图像上,其中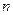 为正整数。
为正整数。
(Ⅰ)证明:数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列。
为等比数列。
(Ⅱ)设(Ⅰ)中“平方递推数列”的前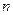 项之积为
项之积为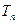 ,即
,即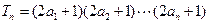 ,求数列
,求数列 的通项及
的通项及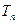 关于
关于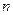 的表达式。
的表达式。
(Ⅲ)记 ,求数列
,求数列 的前
的前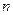 项之和
项之和 ,并求使
,并求使 的
的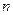 的最小值。
的最小值。
设常数 ,函数
,函数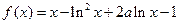
 .
.
(Ⅰ)令
 ,求
,求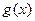 的最小值,并比较
的最小值,并比较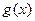 的最小值与零的大小;
的最小值与零的大小;
(Ⅱ)求证: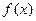 在
在 上是增函数;
上是增函数;
(Ⅲ)求证:当 时,恒有
时,恒有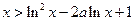 .
.
如图,已知圆O的直径AB=4,定直线L到圆心的距离为4,且直线L垂直直线AB。点P是圆O上异于A、B的任意一点,直线PA、PB分别交L与M、N点。
(Ⅰ)若∠PAB=30°,求以MN为直径的圆方程;
(Ⅱ)当点P变化时,求证:以MN为直径的圆必过圆O内的一定点。
(理)(本题8分)甲、乙、丙三人进行某项比赛,每局有两人参加,没有平局,在一局比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 ,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
,比赛的规则是先由甲和乙进行第一局的比赛,然后每局的获胜者与未参加此局比赛的人进行下一局的比赛,在比赛中,有人获胜两局就算取得比赛的胜利,比赛结束.
(1)求只进行两局比赛,甲就取得 胜利的概率;
胜利的概率;
(2)求只进行两局比赛,比赛就结束的概率;
(3)求甲取得比赛胜利的概率.
20、(文)(本小题8分)甲、乙两人做定点投篮,投篮者若投中则继续投篮,否则由对方投篮,第一次甲投篮,已知甲、乙每次投篮命中的概率分别为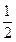 、
、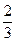 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.
(1)求第三次由乙投篮的概率;
(2)求前4次投篮中各投两次的概率.
(本小题8分)如图,正三棱柱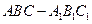 的底面边长为
的底面边长为
 ,侧棱
,侧棱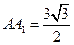 ,
, 是
是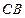 延长线上一点,且
延长线上一点,且

(1)求证:直线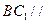 平面
平面 ;
;
(2)求二面角 的大小.
的大小.