（11·十堰）12分）如图，已知抛物线y=x2+bx+c与x轴交于点A（1，0）和点B，与y轴交于点C（0，-3）。
（1）求抛物线的解析式；
（2）如图（1），已知点H（0，-1）.问在抛物线上是否存在点G（点G在y轴的左侧），使得S△GHC=S△GHA？若存在，求出点G的坐标，若不存在，请说明理由；
（3）如图（2），抛物线上点D在x轴上的正投影为点E（-2，0），F是OC的中点，连接DF，P为线段BD上的一点，若∠EPF=∠BDF，求线段PE的长.
已知二次函数
与x轴的公共点有两个。
求：（1）求k的取值范围；
（2）当k=1时，求抛物线与x轴的公共点A和B的坐标及顶点C的坐标；
（3）观察图象，当x取何值时y＞0?
已知关于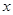
的方程 
.
（1）求证：不论
为任何实数，此方程总有实数根；
（2）若抛物线
与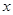轴交于两个不同的整数点，且为正整数，试确定此抛物线的解析式。
某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元。为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。求：
⑴若商场平均每天要盈利1200元，每件衬衫应降价多少元？
⑵每件衬衫降价多少元，商场平均每天盈利最多，最多盈利是多少元？
以△ABC的AB、AC为边分别作正方形ADEB、ACGF，连接DC、BF。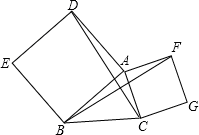
(1)求证：CD＝BF。
(2)利用旋转的观点，在此题中，△ADC可看成由哪个三角形绕哪点旋转多少角度得到的。
现有一块长20cm，宽10cm的长方形铁皮，在它的四个角分别剪去一个大小完全相同的小正方形，用剩余的部分做成一个底面积为56cm2的无盖长方体盒子，求出剪去的小正方形的边长？