(本小题满分12分)已知函数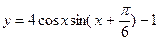
(1)求函数f(x)的最小正周期。
(2)求函数f(x)在区间 上的最大值和最小值。
上的最大值和最小值。
(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某人接受挑战后,对其他3个人发出邀请,记这3个人中接受挑战的人数为ξ,求ξ的分布列和期望;
(Ⅱ)为了解冰桶挑战赛与受邀者的性别是否有关,某机构进行了随机抽样调查,得到如下 列联表:
列联表:
| 接受挑战 |
不接受挑战 |
合计 |
|
| 男性 |
45 |
15 |
60 |
| 女性 |
25 |
15 |
40 |
| 合计 |
70 |
30 |
100 |
根据表中数据,能否在犯错误的概率不超过 的前提下认为“冰桶挑战赛与受邀者的性别有关”?
的前提下认为“冰桶挑战赛与受邀者的性别有关”?
附:
 |
0.100 |
0.050 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
6.635 |
10.828 |
(本小题满分12分)如图,已知正三棱柱 的各棱长均相等,
的各棱长均相等, 是
是 的中点,点
的中点,点 在侧棱
在侧棱 上,且
上,且

(Ⅰ)求证: ⊥
⊥ ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知公差不为零的等差数列 ,满足
,满足 成等比数列.
成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,证明:
,证明: .
.
(本小题满分13分)已知函数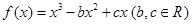 ,其图象记为曲线
,其图象记为曲线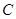 .
.
(Ⅰ)若 在
在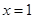 处取得极值为
处取得极值为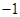 ,求
,求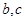 的值;
的值;
(Ⅱ)若 有三个不同的零点,分别为
有三个不同的零点,分别为 ,且
,且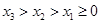 ,过点
,过点 作曲线
作曲线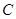 的切线,切点为
的切线,切点为 (点
(点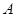 异于点
异于点 ).
).
①证明: ;
;
②若三个零点均属于区间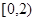 ,求
,求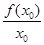 的取值范围.
的取值范围.
(本小题满分13分)已知抛物线的顶点在原点,焦点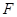 在
在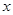 轴上,且抛物线上横坐标为1的点到
轴上,且抛物线上横坐标为1的点到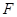 的距离为2 ,过点
的距离为2 ,过点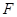 的直线交抛物线于
的直线交抛物线于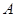 ,
,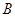 两点.
两点.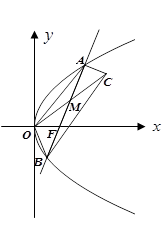
(Ⅰ)求抛物线的方程;
(Ⅱ)若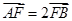 ,求直线
,求直线 的斜率;
的斜率;
(Ⅲ)设点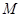 在线段
在线段 上运动,原点
上运动,原点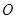 关于点
关于点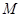 的对称点为
的对称点为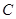 ,求四边形
,求四边形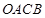 面积的最小值.
面积的最小值.