(本小题满分13分)已知抛物线的顶点在原点,焦点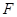 在
在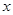 轴上,且抛物线上横坐标为1的点到
轴上,且抛物线上横坐标为1的点到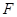 的距离为2 ,过点
的距离为2 ,过点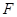 的直线交抛物线于
的直线交抛物线于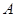 ,
,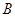 两点.
两点.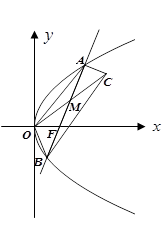
(Ⅰ)求抛物线的方程;
(Ⅱ)若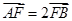 ,求直线
,求直线 的斜率;
的斜率;
(Ⅲ)设点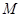 在线段
在线段 上运动,原点
上运动,原点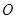 关于点
关于点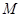 的对称点为
的对称点为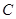 ,求四边形
,求四边形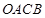 面积的最小值.
面积的最小值.
(本小题满分13分)
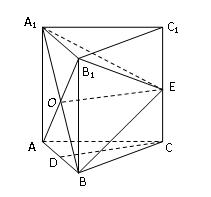
如图,在三棱柱 中,每个侧面均为正方形,
中,每个侧面均为正方形,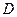 为底边
为底边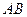 的中点,
的中点, 为侧棱
为侧棱 的中点,
的中点,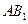 与
与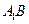 的交点为
的交点为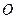 .
.
(Ⅰ)求证: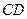 ∥平面
∥平面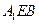 ;
;
(Ⅱ)求证: 平面
平面 .
.
(本小题满分13分)
袋子中装有编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球.
(Ⅰ)写出所有不同的结果;
(Ⅱ)求恰好摸出1个黑球和1个红球的概率;
(Ⅲ) 求至少摸出1个黑球的概率.
(本小题满分13分)
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且
,且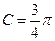 ,
,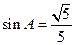 .
.
(Ⅰ)求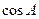 ,
,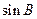 的值;
的值;
(Ⅱ)若 ,求
,求 ,
,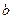 的值.
的值.
(本小题共13分)
已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(Ⅰ)求证:{ }是等差数列;
}是等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若 ,求证:
,求证:  .
.
(本小题共14分)
已知椭圆的中心在原点,焦点在 轴上,经过点
轴上,经过点
 且离心率
且离心率 .过定点
.过定点 的直线与椭圆相交于
的直线与椭圆相交于 ,
, 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)在 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存
的坐标;若不存
在,请说明理由.