在一个暗箱中,放有大小和质量都相同的红、黄、绿、黑四种颜色的球若干个.现从中任意摸出一个球,球摸出后仍放回箱内.若得到红球的概率为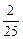 ,得到黄球的概率为
,得到黄球的概率为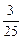 ,得到绿球的概率为
,得到绿球的概率为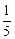 .已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个?
.已知暗箱中黑球有15个,问袋中原有红球、黄球、绿球各多少个?
如图,已知AD是△ABC的中线,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.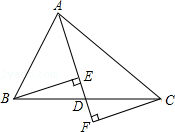
先化简,再求值:(x﹣1)2+x(x+2),其中x=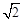 .
.
如图,一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点,与反比例函数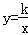 的图象在第一象限内的交点为M(3,m).
的图象在第一象限内的交点为M(3,m).
(1)求反比例函数的解析式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由.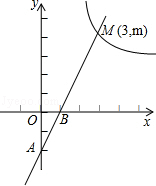
某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 |
2009 |
2010 |
2011 |
2012 |
| 投入技改资金x(万元) |
2.5 |
3 |
4 |
4.5 |
| 产品成本y(万元/件) |
7.2 |
6 |
4.5 |
4 |
(1)试判断:从上表中的数据看出,y与x符合你学过的哪个函数模型?请说明理由,并写出它的解析式.
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
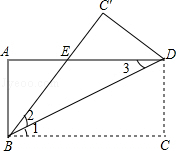
如图所示,将长方形ABCD沿直线BD折叠,使C点落在C′处,BC′交AD于E.
(1)求证:BE=DE;
(2)若AD=8,AB=4,求△BED的面积.