某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
| 年度 |
2009 |
2010 |
2011 |
2012 |
| 投入技改资金x(万元) |
2.5 |
3 |
4 |
4.5 |
| 产品成本y(万元/件) |
7.2 |
6 |
4.5 |
4 |
(1)试判断:从上表中的数据看出,y与x符合你学过的哪个函数模型?请说明理由,并写出它的解析式.
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
若 (x>1)求(1)
(x>1)求(1)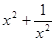 (2)
(2)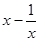 的值.
的值.
如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
(1)解方程:
(2)先化简,再求值: ,其中
,其中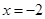 ,
, .
.
(本题14分)已知数轴上有A,B,C三点,分别代表-24,-10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒.
(1)问多少秒后,甲到A,B,C的距离和为40个单位?
(2)若乙的速度为6个单位/秒,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,问甲,乙在数轴上的哪个点相遇?
(3)在(1)(2)的条件下,当甲到A、B、C的距离和为40个单位时,甲调头返回.问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
(本题12分)某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 增减 |
+5 |
-2 |
-4 |
+13 |
-10 |
+16 |
-9 |
(1)根据记录可知前三天共生产辆;
(2)产量最多的一天比产量最少的一天多生产辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?