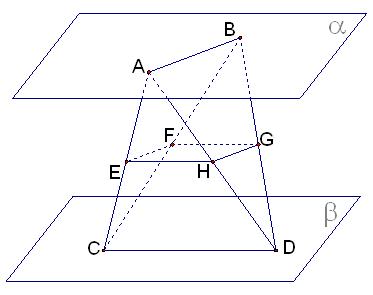
如图:已知平面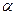 //平面
//平面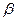 ,点A、B在平面
,点A、B在平面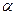 内,点C、D在
内,点C、D在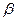 内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
求证:(Ⅰ)E、F、G、H四点共面;
(Ⅱ)平面EFGH//平面 .
.
已知函数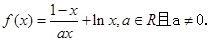
(I)当a=2时,求函数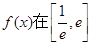 的最大值和最小值;
的最大值和最小值;
(II)若函数 ,求函数
,求函数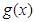 的单调递减区间;
的单调递减区间;
(III)当a=1时,求证: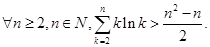
如图为河岸一段的示意图,一游泳者站在河岸的A点处,欲前往河对岸的C点处。若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C。已知此人步行速度为v,游泳速度为0.5v。
(I)设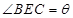 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为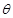 的函数;并求自变量
的函数;并求自变量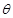 取值范围;
取值范围;
II)当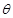 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
定义在R上的单调函数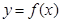 满足
满足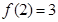 ,且对任意
,且对任意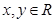 都有
都有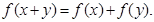
(I)试求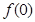 的值并证明函数
的值并证明函数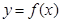 为奇函数;
为奇函数;
(II)若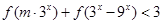 对任意
对任意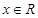 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
已知函数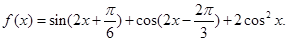
(I)求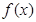 的最大值和最小正周期;
的最大值和最小正周期;
(II)若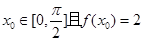 ,求
,求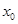 的值。
的值。
已知集合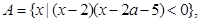 函数
函数 的定义域为集合B。
的定义域为集合B。
(I)若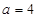 ,求集合
,求集合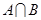 ;
;
(II)已知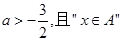 是“
是“ ”的必要条件,求实数a的取值范围。
”的必要条件,求实数a的取值范围。