(本小题14分)已知数列{ }的前
}的前 项和为
项和为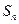 ,且
,且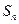 =
= (
(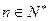 );
); =3
=3
且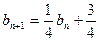 (
(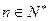 ),
),
(1)写出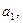


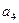 ;
;
(2)求数列{ },{
},{ }的通项公式
}的通项公式 和
和 ;
;
(3)设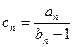 ,求数列
,求数列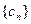 的前
的前 项和
项和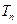 .
.
已知中心在原点,顶点A1、A2在x轴上,离心率e=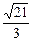 的双曲线过点P(6,6).
的双曲线过点P(6,6).
(1)求双曲线方程.
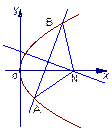
(2)动直线l经过△A1PA2的重心G,与双曲线交于不同的两点M、N,问:是否存在直线l,使G平分线段MN,证明你的结论.
已知双曲线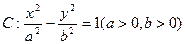 的离心率e=2,A,B为双曲线上两点,线段AB的垂直平分线为
的离心率e=2,A,B为双曲线上两点,线段AB的垂直平分线为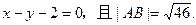
①求双曲线C经过二、四象限的渐近线的倾斜角
②试判断在椭圆C的长轴上是否存在一定点N(a,0),
使椭圆上的动点M满足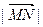 的最小值为3,若存在求出所有可能的a值,若不存在说明理由.
的最小值为3,若存在求出所有可能的a值,若不存在说明理由.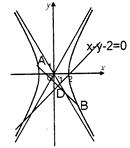
已知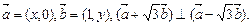
①点P(x,y)的轨迹C的方程;
②若直线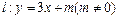 与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.
与曲线C交于A,B两点,D(0,-1)且有|AD|=|BD|,试求m的值.
已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线.
已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B,且|AB|≤2p.
(1)求a的取值范围.
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.