解分式方程: .
.
(梧州)向阳村2010年的人均收入为12000元,2012年的人均收入为14520元,求人均收入的年平均增长率.
(钦州)某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球(每个气排球的价格都相同,每个篮球的价格都相同).经洽谈,购买1个气排球和2个篮球共需210元;购买2个气排球和3个篮球共需340元.
(1)每个气排球和每个篮球的价格各是多少元?
(2)该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个,总费用不超过3200元,且购买气排球的个数少于30个,应选择哪种购买方案可使总费用最低?最低费用是多少元?
(柳州)如图,小黄和小陈观察蜗牛爬行,蜗牛在以A为起点沿直线匀速爬向B点的过程中,到达C点时用了6分钟,那么还需要多长时间才能到达B点?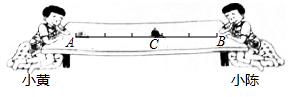
(来宾)已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
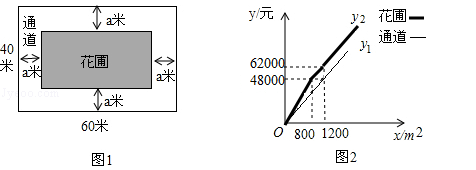
(南宁)如图1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)用含a的式子表示花圃的面积.
(2)如果通道所占面积是整个长方形空地面积的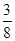 ,求出此时通道的宽.
,求出此时通道的宽.
(3)已知某园林公司修建通道、花圃的造价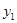 (元)、
(元)、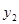 (元)与修建面积x(m2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?
(元)与修建面积x(m2)之间的函数关系如图2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?