已知函数 的图象经过点
的图象经过点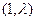 ,且对任意
,且对任意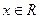 ,都有
,都有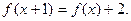 数列
数列 满足
满足
(Ⅰ)当 为正整数时,求
为正整数时,求 的表达式
的表达式
(Ⅱ)设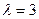 ,求
,求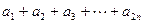
(Ⅲ)若对任意 ,总有
,总有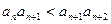 ,求实数
,求实数 的取值范围
的取值范围
已知命题 不等式
不等式 的解集为R;命题
的解集为R;命题 :
: 在区间
在区间 上是增函数.若命题“
上是增函数.若命题“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
已知{ }是公差不为零的等差数列,
}是公差不为零的等差数列, =1,且
=1,且 ,
, ,
, 成等比数列.
成等比数列.
(Ⅰ)求数列{ }的通项;(Ⅱ)求数列{
}的通项;(Ⅱ)求数列{ }的前
}的前 项和
项和 .
.
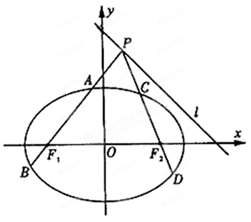
如图,已知椭圆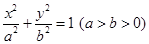 过点.
过点.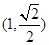 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 、
、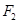 .点
.点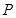 为直线
为直线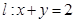 上且不在
上且不在 轴上的任意一点,直线
轴上的任意一点,直线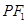 和
和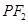 与椭圆的交点分别为
与椭圆的交点分别为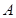 、
、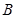 和
和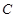 、
、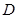 ,
, 为坐标原点.
为坐标原点.
(I)求椭圆的标准方程;
(II)设直线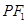 、
、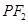 的斜线分别为
的斜线分别为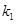 、
、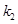 .证明:
.证明: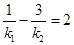
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC= AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
已知{ }是公差不为零的等差数列,
}是公差不为零的等差数列,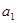 =1,且
=1,且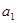 ,
,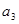 ,
,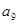 成等比数列.
成等比数列.
(Ⅰ)求数列{ }的通项;(Ⅱ)求数列{
}的通项;(Ⅱ)求数列{ .
.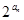 }的前
}的前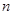 项和
项和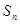 .
.