已知定圆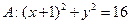 ,动圆
,动圆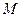 过点
过点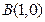 且与圆
且与圆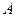 相切,记动圆圆
相切,记动圆圆
心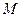 的轨迹为
的轨迹为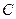 .
.
(Ⅰ)求曲线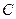 的方程;
的方程;
(Ⅱ)若点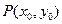 为曲线
为曲线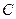 上任意一点,证明直线
上任意一点,证明直线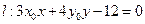 与曲线
与曲线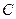 恒有且只有一个公共点.
恒有且只有一个公共点.
设a为实数,函数f(x)=ex-2x+2a,x∈R.
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当a>ln2-1且x>0时,ex>x2-2ax+1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC= ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.
(Ⅰ)证明:AD⊥C1E;
(Ⅱ)当异面直线AC,C1E 所成的角为60°时,求三棱锥C1-A1B1E的体积.
在等差数列{an}中,a2+a7=-23,a3+a8=-29.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求数列{bn}的前n项和Sn.
设△ABC的内角A,B,C的对边分别为a,b,c,(a+b+c)(a-b+c)=ac.
(Ⅰ)求B;
(Ⅱ)若sinAsinC= ,求C.
,求C.
已知函数f(x)的导函数为f ′(x),且对任意x>0,都有f ′(x)> .
.
(Ⅰ)判断函数F(x)= 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(Ⅱ)设x1,x2∈(0,+∞),证明:f(x1)+f(x2)<f(x1+x2);
(Ⅲ)请将(Ⅱ)中的结论推广到一般形式,并证明你所推广的结论.