某市为了争创“全国文明城市”,市文明委组织了精神文明建设知识竞赛。统 计局调查队随机抽取了甲、乙两队中各6名组员的成绩,得分情况如下表所示:
计局调查队随机抽取了甲、乙两队中各6名组员的成绩,得分情况如下表所示:
| 甲组 |
84 |
85 |
87 |
88 |
88 |
90 |
| 乙组 |
82 |
86 |
87 |
88 |
89 |
90 |
(1) 根据表中的数据,哪个组对精神文明建设知识的掌握更为稳定?
(2) 用简单随机抽样方法从乙组6名成员中抽取两名,他们的得分情况组成一个样本,求抽
出的两名成员的分数差值至少是4分的概率。
本小题满分12分)
对于任意的实数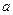 ,不等式
,不等式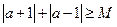 恒成立,记实数
恒成立,记实数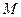 的最大值是
的最大值是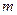 .
.
(1)求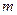 的值;
的值;
(2)解不等式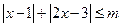 .
.
(本小题满分12分)
已知数列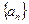 满足
满足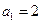 ,且
,且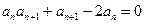 (
(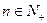 )。
)。
(1)求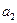 、
、 、
、 的值;
的值;
(2)猜想数列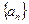 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
(本小题满分12分)
已知投资某项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是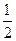 .设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为
.设该项目产品价格在一年内进行2次独立的调整,记产品价格在一年内的下降次数为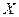 ,对该项目每投资十万元,
,对该项目每投资十万元,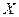 取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
取0、1、2时,一年后相应的利润为1.6万元、2万元、2.4万元.求投资该项目十万元,一年后获得利润的数学期望及方差.
(本小题满分10分)
某班组织知识竞赛,已知题目共有10道,随机抽取3道让某人回答,规定至少要答对其中2道才能通过初试,他只能答对其中6道,试求:
(1)抽到他能答对题目数的分布列;
(2)他能通过初试的概率。
已知抛物线 :
: 上一点
上一点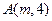 到其焦点的距离为
到其焦点的距离为 .
.
(I)求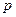 与
与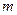 的值;
的值;
(II)设抛物线 上一点
上一点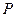 的横坐标为
的横坐标为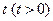 ,过
,过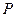 的直线交
的直线交 于另一点
于另一点 ,交
,交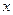 轴于点
轴于点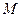 ,过点
,过点 作
作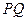 的垂线交
的垂线交 于另一点
于另一点 .若
.若 是
是 的切线,求
的切线,求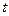 的最小值.
的最小值.