若函数 为定义域
为定义域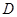 上的单调函数,且存在区间
上的单调函数,且存在区间 (其中
(其中 ,使得当
,使得当 时,
时,  的取值范围恰为
的取值范围恰为 ,则称函数
,则称函数 是
是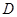 上的正函数,区间
上的正函数,区间 叫做函数的等域区间.
叫做函数的等域区间.
已知 是
是 上的正函数,求
上的正函数,求 的等域区间;
的等域区间;
试探求是否存在 ,使得函数
,使得函数 是
是 上的正函数?若存在,请求出实数
上的正函数?若存在,请求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知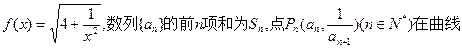
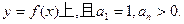
(I)求数列{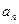 }的通项公式
}的通项公式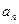 ;
;
(II)数列{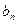 }的首项b1=1,前n项和为Tn,且
}的首项b1=1,前n项和为Tn,且 ,求数列{
,求数列{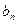 }的通项公式bn.
}的通项公式bn.
某班从6名干部中(其中男生4人,女生2人),选3人参加学校的义务劳动.
(I)设所选3人中女生人数为ξ,求ξ的分布列及Eξ;
(II)求男生甲或女生乙被选中的概率;
(III)在男生甲被选中的情况下,求女生乙也被选中的概率.
如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB,PB的中点.
(I)求证:EF⊥CD;
(II)求DB与平面DEF所成角的正弦值;
(III)在平面PAD内是否存在一点G,使G在平面PCB上的射影为△PCB的外心,若存在,试确定点G的位置;若不存在,说明理由.
已知△ABC的面积S满足
(I)求 的取值范围;
的取值范围;
(2)求函数 的最大值.
的最大值.
在⊿ABC中,角A、B、C所对的边分别为a、b、c,且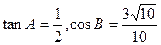
(1)求tanC的值;(2)若⊿ABC最长的边为1,求b。