(本小题满分12分)
如图,四棱锥 ,
, ≌
≌ ,在它的俯视图
,在它的俯视图 中,
中, ,
, ,
,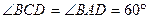 .
.
⑴求证: 是直角三角形;⑵求四棱锥
是直角三角形;⑵求四棱锥 的体积.
的体积.
(本小题满分14分)设函数 ,
,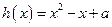 .
.
(Ⅰ)当 时,
时,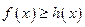 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,若函数
时,若函数 在
在 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 的取值
的取值 范围;
范围;
(Ⅲ)是否存在实数 ,使函数
,使函数 和函数
和函数 在公共定义域上具有相同的单调性?若存在,求出
在公共定义域上具有相同的单调性?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(本小题满分13分)某巡逻艇在A处发现北偏东45 相距9海里的C处有一艘走私船,正沿南偏东75
相距9海里的C处有一艘走私船,正沿南偏东75 的方向以10海里/小时的速度逃窜.
的方向以10海里/小时的速度逃窜.
(Ⅰ)若巡逻艇计划在正东方向进行拦截,问巡逻艇应行驶到什么位置进行设卡?
(Ⅱ)若巡逻艇立即以14海里/小时的速度沿着直线方向追击,问经多少时间后巡逻艇恰追赶上该走私船?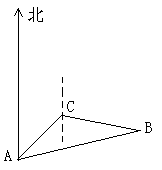
(本小题满分13分)
如图, 是单位圆与
是单位圆与 轴正半轴的交点,
轴正半轴的交点, ,
,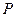 为单位圆上不同的点,
为单位圆上不同的点, ,
, ,
, ,
,
(Ⅰ)当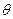 为何值时,
为何值时, ?
?
(Ⅱ)若 ,则当
,则当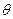 为何值时,点
为何值时,点 在单位圆上?
在单位圆上?
(本小题满分13分)
已知函数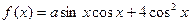 ,
, ,
,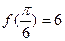 .
.
(Ⅰ)求常数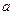 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数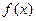 的最小正周期和最大值.
的最小正周期和最大值.
设椭圆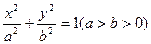 的焦点分别为
的焦点分别为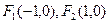 ,直线
,直线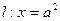 交
交 轴于点
轴于点 ,且
,且 .
.
(1)试求椭圆的方程;
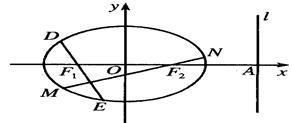
(2)过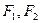 分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形
分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形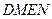 面积的最大值和最小值.
面积的最大值和最小值.