本题满分12分)
已知函数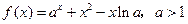
(Ⅰ)求证:函数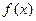 在
在 上单调递增;
上单调递增;
(Ⅱ)对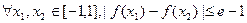 恒成立,求
恒成立,求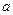 的取值范围.
的取值范围.
(本题共12分)
(1)计算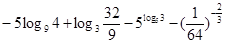
(2)解方程: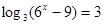
(本题共12分)设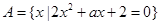 ,
,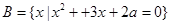 ,
, 。
。
(1)求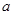 的值及
的值及 ;
;
(2)设全集 ,求 (∁I A)
,求 (∁I A) (∁I B);
(∁I B);
(3)写出(∁I A) (∁I B)的所有子集。
(∁I B)的所有子集。
如图,等腰梯形ABEF中,AB//EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
(1)求证:AF⊥平面CBF;
(2)在棱FC上是否存在点M,使得OM//平面DAF?
(3)求点A到平面BDF的距离.
已知直线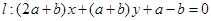 .
.
(1)证明直线 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(2)求直线 与第二象限所围成三角形的面积的最小值,并求面积最小时直线
与第二象限所围成三角形的面积的最小值,并求面积最小时直线 的方程.
的方程.
正三棱柱 中,点
中,点 是
是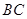 的中点,
的中点,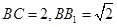 .
.
(1)求证: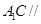 平面
平面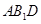 ;
;
(2)求证: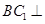 平面
平面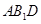 .
.