从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度x与底面正方形的边长的比不超过常数t.
问:(1)求长方体的容积V关于x的函数表达式;(2)x取何值时,长方体的容积V有最大值?

如图,矩形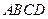 的两条对角线相交于点
的两条对角线相交于点 ,
,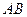 边所在直线的方程为
边所在直线的方程为 点
点 在
在 边所在直线上.
边所在直线上.
(I)求 边所在直线的方程;
边所在直线的方程;
(II)求矩形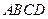 外接圆的方程;
外接圆的方程;
(III)若动圆 过点
过点 ,且与矩形
,且与矩形 的外接圆外切,求动圆
的外接圆外切,求动圆 的圆心的轨迹方
的圆心的轨迹方
程.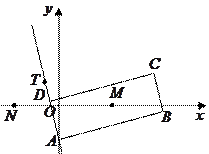
如图, 为空间四点.在
为空间四点.在 中,
中,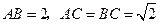 .等
.等
边三角形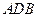 以
以 为轴运动.
为轴运动.
(Ⅰ)当平面 平面
平面 时,求
时,求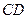 ;
;
(Ⅱ)当 转动时,是否总有
转动时,是否总有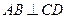 ?证明你的结论.
?证明你的结论.

有时可用函数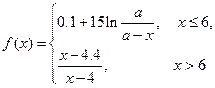
述学习某学科知识的掌握程度.其中 表示某学科知识的学习次数(
表示某学科知识的学习次数( ),
), 表示对该学科知识的掌握程度,正实数a与学科知识有关
表示对该学科知识的掌握程度,正实数a与学科知识有关
(1)证明:当x  7时,掌握程度的增长量f(x+1)- f(x)总是下降;
7时,掌握程度的增长量f(x+1)- f(x)总是下降;
(2)根据经验,学科甲、乙、丙对应的a的取值区间分别为(115,121],(12 1,127]
1,127]
(127,133].当学习某学科知识6次时,掌握程度是 85%,请
85%,请 确定相应的学科.
确定相应的学科.