已知:等差数列{ }中,
}中,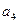 =14,前10项和
=14,前10项和 .
.
(1)求 ;
;
(2)将{ }中的第2项,第4项,…,第
}中的第2项,第4项,…,第 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前 项和
项和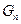 .
.
(本小题满分14分)设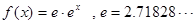 是自然对数的底.
是自然对数的底.
(1)求曲线 在点
在点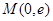 处的切线方程;
处的切线方程;
(2)设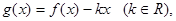 试探究函数
试探究函数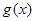 的单调性;
的单调性;
(3)若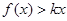 总成立,求
总成立,求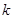 的取值范围.
的取值范围.
(本小题满分14分)已知抛物线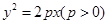 的焦 点为F,A是抛物线上横坐标为4、
的焦 点为F,A是抛物线上横坐标为4、
位于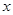 轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于
轴上方的点,A到抛物线准线的距离等于5.过A作AB垂直于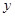 轴,垂足为B,OB的中点为M.
轴,垂足为B,OB的中点为M.
(1)求抛物线方程.
(2)以M为圆心,MB为半径作圆M,当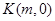 是
是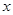 轴上一动点时,讨论直线AK与圆M的位置关系.
轴上一动点时,讨论直线AK与圆M的位置关系.
(本小题满分14分)已知等差数列 的各项均为正数,
的各项均为正数,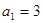 ,前n项和为Sn,数列
,前n项和为Sn,数列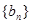 是等比数列,
是等比数列,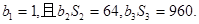
(1)求数列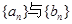 的通项公式.
的通项公式.
(2)求证: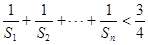 对一切
对一切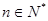 都成立.
都成立.
(本小题满分14分)如图,平行四边形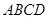 中,
中,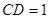 ,
,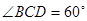 ,且
,且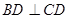 ,
,
正方形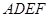 和平面
和平面 成直二面角,
成直二面角, 是
是 的中点.
的中点.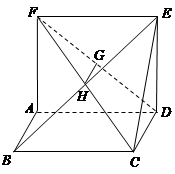
(1)求证: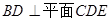 .
.
(2)求证: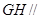 平面
平面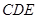 .
.
(3)求三棱锥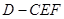 的体积.
的体积.
(本小题满分12分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到如下的列联表:
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
(3)为了研究喜欢打蓝球是否与性别有关,计算出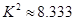 ,你有多大的把握认为是否喜欢打蓝球与性别有关?
,你有多大的把握认为是否喜欢打蓝球与性别有关?
附:(临界值表供参考)
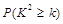 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
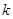 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |