(本小题满分12分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
(3)为了研究喜欢打蓝球是否与性别有关,计算出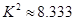 ,你有多大的把握认为是否喜欢打蓝球与性别有关?
,你有多大的把握认为是否喜欢打蓝球与性别有关?
附:(临界值表供参考)
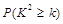 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
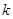 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
(1)指出这组数据的众数和中位数;
(2)若视力测试结果不低于5.0,则称为“good sight”,若校医从“good sight”,中随机选取2人,试求抽到视力有5.2的学生的概率。
已知函数 .
.
(Ⅰ)若点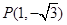 在角
在角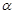 的终边上,求
的终边上,求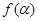 的值;
的值;
(Ⅱ)若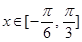 ,求
,求 的值域.
的值域.
(14分)已知定义在R上的函数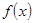 对任意
对任意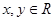 都有
都有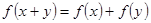 ,且当
,且当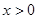 时,
时,
(1)求证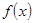 为奇函数;
为奇函数;
(2)判断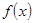 在R上的单调性,并用定义证明;
在R上的单调性,并用定义证明;
(3)若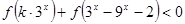 ,对任意
,对任意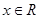 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知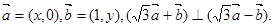
(1)求点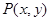 的轨迹C的方程;
的轨迹C的方程;
(2)若直线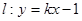 与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实数k的取值范围.
与曲线C交于A、B两点,并且A、B在y轴的同一侧,求实数k的取值范围.
(3)设曲线C与x轴的交点为M,若直线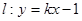 与曲线C交于A、B两点,是否存在实数k,使得以AB为直径的圆恰好过点M?若有,求出k的值;若没有,写出理由.
与曲线C交于A、B两点,是否存在实数k,使得以AB为直径的圆恰好过点M?若有,求出k的值;若没有,写出理由.
数列{an}满足
(1) 求数列{an}的通项公式;
(2) 若数列{bn}满足: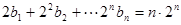 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3) 令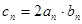 (n∈N*),求数列{cn}的前n项和Tn.
(n∈N*),求数列{cn}的前n项和Tn.