由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
(1)指出这组数据的众数和中位数;
(2)若视力测试结果不低于5.0,则称为“good sight”,若校医从“good sight”,中随机选取2人,试求抽到视力有5.2的学生的概率。
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列.
的分布列.
已知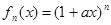 ,且
,且 展开式的各式系数和为243.
展开式的各式系数和为243.
(I)求a的值。
(II)若 ,求
,求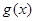 中含
中含 的系数。
的系数。
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为 .
.
(Ⅰ)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最值;
(Ⅲ)请问是否存在直线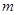 ,
,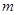 ∥l且
∥l且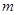 与曲线C的交点A、B满足
与曲线C的交点A、B满足 ;
;
若存在请求出满足题意的所有直线方程,若不存在请说明理由。
如图,过抛物线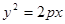 (
( >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标;
⑵求弦AB中点M的轨迹方程。
在平面直角坐标系xOy中,圆C的参数方程为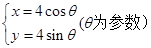 ,直线l经过点P(2,2),倾斜角
,直线l经过点P(2,2),倾斜角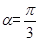 。
。
(1)写出圆的标准方程和直线l的参数方程;
(2)设l与圆C相交于A、B两点,求 的值。
的值。