（本小题满分14分）设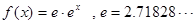
是自然对数的底．
（1）求曲线
在点
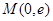处的切线方程；
（2）设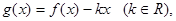
试探究函数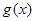
的单调性；
（3）若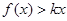
总成立，求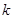
的取值范围．
已知函数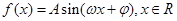
（其中A>0, ω>0,0<
<
）的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为
.
（1）求f（x）的解析式；
（2）当
，求f（x）的值域.
已知函数
（1）求函数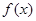
的最大值和最小值以及取最大、最小值时相应
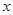的取值集合；
（2）写出函数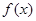的单调递增区间．
（3）作出此函数在一个周期内的图像。
已知函数
且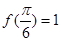
（1）求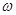
的最小值及此时函数
的表达式
（2）将（1）中所得函数的图像结果怎样变换可得
的图像
已知角
的终边经过点P（
，3），
（1）求
的值;
（2）求
的值.
（本小题满分14分）已知函数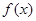
是定义域为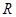
的偶函数，当
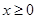时，
．
（1）在给定的图示中画出函数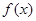的图象（不需列表）；
（2）求函数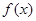的解析式；
（3）讨论方程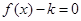
的根的情况。（只需写出结果，不要解答过程)