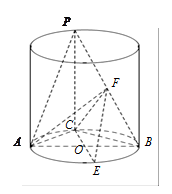
如图所示,圆柱底面的直径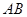 长度为
长度为 ,
, 为底面圆心,正三角形
为底面圆心,正三角形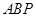 的一个顶点
的一个顶点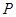 在上底面的圆周上,
在上底面的圆周上, 为圆柱的母线,
为圆柱的母线,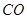 的延长线交
的延长线交 于点
于点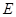 ,
,  的中点为
的中点为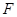 .
.
(1)求证:平面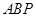 ⊥平面
⊥平面 ;
;
(2)求二面角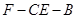 的正切值.
的正切值.
在我市“城乡清洁工程”建设活动中,社会各界掀起净化美化环境的热潮.某单位计划在小区内种植 四棵风景树,受本地地理环境的影响,
四棵风景树,受本地地理环境的影响, 两棵树的成活的概率均为
两棵树的成活的概率均为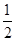 ,另外两棵树
,另外两棵树 为进口树种,其成活概率都为
为进口树种,其成活概率都为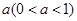 ,设
,设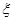 表示最终成活的树的数量.
表示最终成活的树的数量.
(1)若出现 有且只有一颗成活的概率与
有且只有一颗成活的概率与 都成活的概率相等,求
都成活的概率相等,求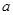 的值;
的值;
(2)求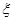 的分布列(用
的分布列(用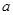 表示);
表示);
(3)若出现恰好两棵树成活的的概率最大,试求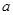 的取值范围.
的取值范围.
在平面直角坐标系上,设不等式组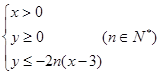 表示的平面区域为
表示的平面区域为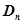 ,记
,记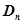 内的整点(横坐标和纵坐标均为整数的点)的个数为
内的整点(横坐标和纵坐标均为整数的点)的个数为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若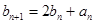 ,
, .求证:数列
.求证:数列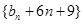 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式.
的通项公式.
已知函数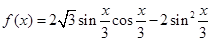 .
.
(1)求函数 的值域;
的值域;
(2)在△ 中,角
中,角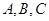 所对的边分别为
所对的边分别为 ,若
,若 ,且
,且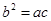 ,求
,求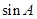 的值
的值
已知函数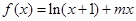 ,当
,当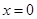 时,函数
时,函数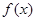 取得极大值.
取得极大值.
(1)求实数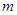 的值;
的值;
(2)已知结论:若函数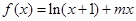 在区间
在区间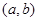 内导数都存在,且
内导数都存在,且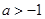 ,则存在
,则存在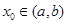 ,使得
,使得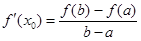 .试用这个结论证明:若
.试用这个结论证明:若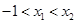 ,函数
,函数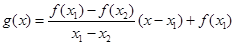 ,则对任意
,则对任意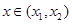 ,都有
,都有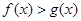 ;
;
(3)已知正数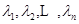 ,满足
,满足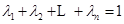 ,求证:当
,求证:当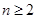 ,
,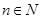 时,对任意大于
时,对任意大于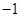 ,且互不相等的实数
,且互不相等的实数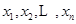 ,都有
,都有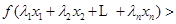
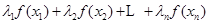 .
.