做投掷2颗骰子试验，用（
x,y）表示点P的坐标，其中x表示第1颗骰子出现的点数，y表示第2颗骰子出现的点数.
（1）求点P在直线y=x上的概率
（2）求点P不在直线y=x+1上的概率
（3）求
点P的坐标（x,y）满足16<
的概率
已知数列
中，前
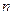项和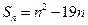
（1）求这个数列的通项公式，并证明该数列是等差数列；
（2）当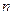为何值时，
取得最小值，此时最小值是多少。
（本小题满分12分）
已知函数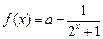
.；
（1）确定
的值，使
为奇函数；
（2）当为奇函数时，求的值域.
（本小题满分12分）某产品按质量分为10个档次，生产第一档（即最低档次）的利润是每件8元，每提高一个档次，利润每件增加2元，但每提高一个档次，在相同的时间内，产量减少3件。如果在规定的时间内，最低档次的产品可生产60件
（I）请写出相同时间内产品的总利润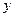
与档次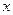
之间的函数关系式，并写出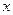的定义域
（II）在同样的时间内，生产哪一档次产品的总利润最大？并求出最大利润.
（本小题满分12分）已知函数
（1）判断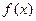
的奇偶性，并证明你的结论；
（2）证明：函数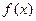在
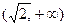内是增函数
(本小题满分10分)
（1）计算：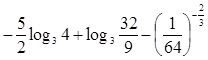
（2）已知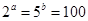
求
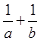的值