(本题8分)已知等差数列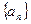 满足:
满足: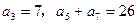 ,
,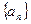 的前
的前 项和为
项和为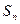 。
。
(1)求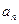 及
及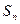 ;
;
(2)令 (其中
(其中 为常数,且
为常数,且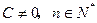 ),求证数列
),求证数列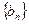 为等比数列。
为等比数列。
已知函数f(x)=x3+ax2+b的图象在点P(1,0)处的切线与直线3x+y=0平行,
(1)求常数a、b的值;
(2)求函数f(x)在区间[0,t]上的最小值和最大值。(t>0)
已知椭圆C: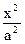 +
+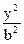 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为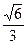 ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
(1)求直线ON(O为坐标原点)的斜率KON ;
(2)对于椭圆C上任意一点M,试证:总存在角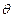 (
(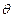 ∈R)使等式:
∈R)使等式: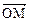 =cos
=cos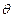
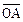 +sin
+sin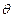
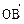 成立。
成立。
已知过点A(0,1),且方向向量为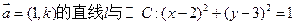 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数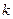 的取值范围;
的取值范围;
(2)求证: ;
;
(3)若O为坐标原点,且 .
.
学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟,课后研讨20分钟,可获得学分5分;B套选修课播32分钟,课后研讨40分钟,可获学分4分。全学期20周,网络每周开播两次,每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟,研讨时间不得少于1000分钟。两套选修课怎样合理选择,才能获得最好学分成绩?
本地一公司计划2008年在省、市两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,省、市电视台的广告收费标准分别为 元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?