(本小题满分13分)
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的
绝对值不超过5的概率。
(参考数据:

 ,
,
参考公式:回归直线方程 ,其中
,其中 )
)
已知函数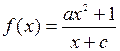
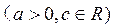 为奇函数,当
为奇函数,当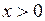 时,
时, 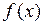 的最小值为2.
的最小值为2.
(I)求函数的解析式
(Ⅱ)若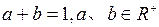 ,求证:
,求证: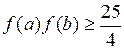
(Ⅲ) 若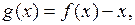
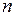
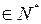 且
且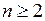 ,求证:
,求证: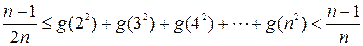
为了竖一块广告牌,要制造三角形支架 ,三角形支架如图所示 . 要求∠ACB=60°,BC长度大于 1 米,且AC比AB长 0.5 米 . 为了广告牌稳固,要求AC 的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
已知f(x)=2cos2x+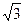 sin2x+a (a∈R , a为常数)
sin2x+a (a∈R , a为常数)
(Ⅰ) 若x∈R , 求f(x)的单调增区间;
(Ⅱ) 若x∈[0, 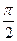 ]时, f(x)的最大值为4, 并求此时f(x)的最小值。
]时, f(x)的最大值为4, 并求此时f(x)的最小值。
已知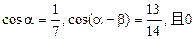 <
< <
< <
<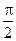 ,
,
( Ⅰ)求
Ⅰ)求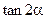 的值.
的值.
(Ⅱ)求
 .
.
如图,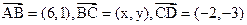

(Ⅰ)若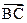 ∥
∥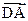 ,求x与y间的关系
,求x与y间的关系
(Ⅱ)在(I)的条件下,若有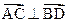 ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.