(本小题满分12分)
某单位组织50名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,创导文明新风;2、到指定的社区、车站、码头做义工,帮助那些需要帮助的人。各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| |
宣传慰问 |
义工救助 |
总计 |
| 20至40岁 |
11 |
16 |
27 |
| 大于40岁 |
15 |
8 |
23 |
| 总计 |
26 |
24 |
50 |
(Ⅰ) 用分层抽样方法在做义工的志愿者中随机抽取6名,大于40岁的应该抽取几名?
(Ⅱ) 在上述抽取的6名志愿者中任取2名,求恰有1名志愿者年龄大于40岁的概率.
(Ⅲ)如果“宣传慰问”与“做义工”是两个分类变量,并且计算出随机变量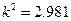 ,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
已知圆的极坐标方程为: 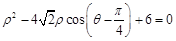 .
.
⑴将极坐标方程化为普通方程;
⑵若点P(x,y)在该圆上,求x+y的最大值和最小值.
已知矩阵A=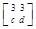 ,若矩阵A属于特征值6的一个特征向量为α1=
,若矩阵A属于特征值6的一个特征向量为α1= ,属于特征值1的一个特征向量为α2=
,属于特征值1的一个特征向量为α2=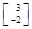 .求矩阵A,并写出A的逆矩阵.
.求矩阵A,并写出A的逆矩阵.
(本小题满分16分)
已知 ,
,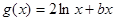 ,且直线
,且直线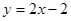 与曲线
与曲线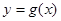 相切.
相切.
(1)若对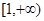 内的一切实数
内的一切实数 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)当 时,求最大的正整数
时,求最大的正整数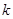 ,使得对
,使得对 (
( 是自然对数的底数)内的任意
是自然对数的底数)内的任意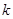 个实数
个实数 都有
都有 成立;
成立;
(3)求证:
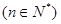 .
.
已知有穷数列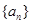 共有
共有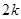 项(整数
项(整数 ),首项
),首项 ,设该数列的前
,设该数列的前 项和为
项和为 ,且
,且 其中常数
其中常数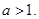 ⑴求
⑴求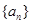 的通项公式;⑵若
的通项公式;⑵若 ,数列
,数列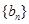 满足
满足
求证: ;
;
⑶若⑵中数列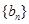 满足不等式:
满足不等式: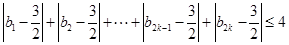 ,求
,求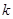 的最大值.
的最大值.
(本小题满分15分)
给定椭圆C: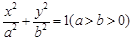 ,称圆心在原点O、半径是
,称圆心在原点O、半径是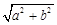 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为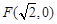 ,其短轴的一个端点到点
,其短轴的一个端点到点 的距离为
的距离为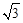 .
.
(1)求椭圆C和其“准圆”的方程;
(2)若点 是椭圆C的“准圆”与
是椭圆C的“准圆”与 轴正半轴的交点,
轴正半轴的交点,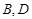 是椭圆C上的两相异点,且
是椭圆C上的两相异点,且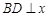 轴,求
轴,求 的取值范围;
的取值范围;
(3)在椭圆C的“准圆”上任取一点 ,过点
,过点 作直线
作直线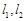 ,使得
,使得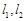 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断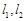 是否垂直?并说明理由.
是否垂直?并说明理由.