((本小题满分14分)
(1)某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了 名员工进行调查,所得的数据如下表所示:
名员工进行调查,所得的数据如下表所示:
| 积极支持改革 |
不太支持改革 |
合计 |
|
| 工作积极 |
 |
 |
 |
| 工作一般 |
 |
 |
 |
| 合计 |
 |
 |
 |
对于人力资源部的研究项目,根据上述数据你能得出什么结论?
(友情提示:当 时,有
时,有 的把握说事件
的把握说事件 与
与 有关;当
有关;当 时,有
时,有 的把握说事件
的把握说事件 与
与 有关; 当
有关; 当 时认为事件
时认为事件 与
与 无关.)
无关.)
(2)高中数学必修3第三章内容是概率.概率包括事件与概率,古典概型,概率的应用.事件与概率又包括随机现象,事件与基本事件空间,频率与概率,概率的加法公式.请画出它们之间的知识结构图.
设函数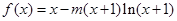 ,其中
,其中 为非负实数.
为非负实数.
(Ⅰ)求 的极大值;
的极大值;
(Ⅱ)当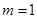 时,若直线
时,若直线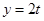 与函数
与函数 在
在 上的图象有交点,求实数
上的图象有交点,求实数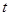 的取值范围;
的取值范围;
(Ⅲ)证明:当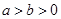 时,
时,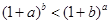 .
.
已知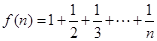 .经计算得
.经计算得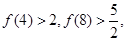
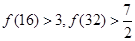 .
.
(Ⅰ)由上面数据,试猜想出一个一般性结论;
(Ⅱ)用数学归纳法证明你的猜想.
已知曲线 在
在 处的切线与直线
处的切线与直线 垂直.
垂直.
(Ⅰ)求 解析式;
解析式;
(Ⅱ)求 的单调区间并画出
的单调区间并画出 的大致图象;
的大致图象;
(Ⅲ)已知函数 ,若对任意
,若对任意 ,总有
,总有
 求实数
求实数 的取值范围.
的取值范围.
某区要进行中学生篮球对抗赛,为争夺最后一个小组赛名额,甲、乙、丙三支篮球队要进行比赛,根据规则:每两支队伍之间都要比赛一场;每场比赛胜者得 分,负者得
分,负者得 分,没有平局,获得第一名的将夺得这个参赛名额.已知乙队胜丙队的概率为
分,没有平局,获得第一名的将夺得这个参赛名额.已知乙队胜丙队的概率为 ,甲队获得第一名的概率为
,甲队获得第一名的概率为 ,乙队获得第一名的概率为
,乙队获得第一名的概率为 .
.
(Ⅰ)求甲队分别战胜乙队和丙队的概率 ;
;
(Ⅱ)设在该次比赛中,甲队得分为 ,求
,求 的分布列及期望.
的分布列及期望.