图中各正方形图案,每条边上有 个圆点,第
个圆点,第 个图案中圆点的总数是
个图案中圆点的总数是 .
.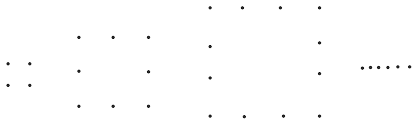
n=2 n=3 n=4
按此规律推断出 与
与 的关系式为
的关系式为
A. = =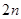 |
B. =4n-4 =4n-4 |
C. = = |
D. = = |
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日到3日的每天昼夜温差与实验室每天每100颗种子发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
| 温差x(0C) |
11 |
13 |
12 |
| 发芽数y(颗) |
25 |
30 |
26 |
该农科所确定的研究方案是:先从这3组数据求出线性回归方程,再对12月4日的数据进行推测和检验.则根据以上3天的数据,求出y关于x的线性回归方程是
A. 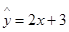
B. 
C. 
D. 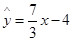
如图3,在半径为 R的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是
R的圆内随机撒一粒黄豆,它落在阴影部分内接正三角形上的概率是
A. |
B.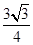 |
C.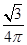 |
D. |
从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是
| A.1 | B.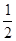 |
C. |
D.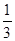 |
某雷达测速区规定:凡车速大于或等于70km/h的汽车视为“超速”,并将受到处罚,如图2是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看得出将被处罚的汽车大约有 
A. 辆 辆 |
B.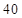 辆 辆 |
C.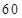 辆 辆 |
D.80辆 |