(本小题满分12分) 已知函数f(x)=ax2+bx+c(a>0,b∈R, c∈R).
(Ⅰ)若函数f(x)的最小值是f(-1)=0,且c=1,
,
求F(2)+F(-2)的值
(Ⅱ)若a=1,c=0,且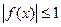
在区间(0,1]上恒成立，试求b的取值范围。
（本小题满分10分）已知
≤
≤1，若函数
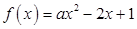在区间[1，3]上的最大值为
，最小值为
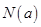，令
．
（1）求
的函数表达式；
（2）写出函数单调增区间与单调减区间（不必证明），并求出的最小值
（本小题满分10分）函数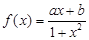
是定义在（－1,1）上的奇函数，且
．
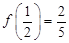（1）确定函数f（x）的解析式；
（2）用定义证明f（x）在（－1,1）上是增函数；
（3）解不等式：f（t－1）＋f（t）＜0．
（本小题满分8分）某市出租车的计价标准是：4km以内10元（含4km），超过4km且不超过18km的部分1．2元/km；超出18km的部分1．8元/km。
（1）如果不计等待时间的费用，建立车费y与行车里程x的函数关系；
（2）如果某人乘车行驶了20km，他要付多少车费？
（本小题满分8分）已知集合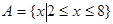
, 
, 
,
．
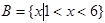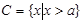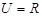（1）求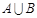
，（CUA）
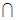B；
（2）如果
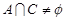，求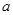
的取值范围．
四棱柱ABCD－A1B1C1D1的三视图和直观图如下．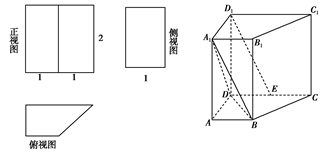
（1）求出该四棱柱的表面积；
（2）设E是DC上一点，试确定E的位置，使D1E∥平面A1BD，并说明理由．