以平面直角坐标系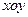 的原点
的原点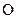 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为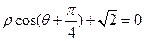 ,曲线
,曲线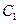 的参数方程为
的参数方程为 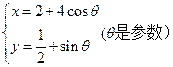
(1)若把曲线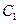 上的横坐标缩短为原来的
上的横坐标缩短为原来的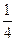 ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线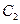 ,
,
求曲线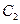 在直角坐标系下的方程
在直角坐标系下的方程
(2)在第(1)问的条件下,判断曲线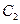 与直线
与直线 的位置关系,并说明理由;
的位置关系,并说明理由;
柜子里有 双不同的鞋,随机地取出
双不同的鞋,随机地取出 只,记事件
只,记事件 表示“取出的鞋配不成对”;事件
表示“取出的鞋配不成对”;事件 表示“取出的鞋都是同一只脚的”;事件
表示“取出的鞋都是同一只脚的”;事件 表示“取出的鞋一只是左脚的,一只是右脚的,但配不成对”.
表示“取出的鞋一只是左脚的,一只是右脚的,但配不成对”.
(Ⅰ)请列出所有的基本事件;
(Ⅱ)分别求事件 、事件
、事件 、事件
、事件 的概率.
的概率.
甲、乙两同学的6次考试成绩分别为:
| 甲 |
 |
 |
 |
 |
 |
 |
| 乙 |
 |
 |
 |
 |
 |
 |
(Ⅰ)画出甲、乙两同学6次考试成绩的茎叶图;
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
已知非零向量 ,
, 满足
满足 且
且 .
.
(Ⅰ)若 ,求向量
,求向量 ,
, 的夹角;
的夹角;
(Ⅱ)在(Ⅰ)的条件下,求 的值.
的值.
化简:(Ⅰ) ;
;
(Ⅱ) .
.
各项均为正数的数列 中,
中,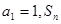 是数列
是数列 的前
的前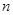 项和,对任意
项和,对任意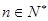 ,有
,有 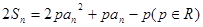 ;
;
(1)求常数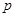 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)记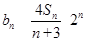 ,求数列
,求数列 的前
的前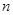 项和
项和 。
。