(本小题满分12分)
已知 是数列
是数列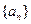 其前
其前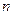 项和,且
项和,且 ,
, .
.
(1)求数列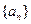 的通项公式;
的通项公式;
(2)设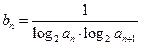 ,且
,且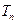 是数列
是数列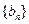 的前
的前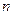 项和,求使得
项和,求使得 对所有
对所有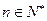 都成立的最小正整数
都成立的最小正整数 .
.
(本小题满分12分)
已知函数 的最大值为
的最大值为 ,
,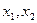 是集合
是集合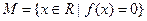 中的任意两个元素,且|
中的任意两个元素,且|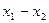 |的最小值为
|的最小值为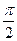 。
。
(I)求 ,
, 的值;
的值;
(II)若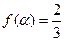 ,求
,求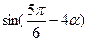 的值
的值
已知 R,函数
R,函数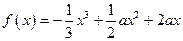 (x∈R).
(x∈R).
(Ⅰ)当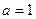 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)函数 是否在R上单调递减,若是,求出
是否在R上单调递减,若是,求出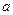 的取值范围;若不是,请说明理由;
的取值范围;若不是,请说明理由;
(Ⅲ)若函数 在
在 上单调递增,求
上单调递增,求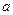 的取值范围.
的取值范围.
某工厂日生产某种产品最多不超过30件,且在生产过程中次品率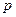 与日产量
与日产量 (
( )件间的关系为
)件间的关系为  ,每生产一件正品盈利2900元,每出现一件次品亏损1100元.
,每生产一件正品盈利2900元,每出现一件次品亏损1100元.
(Ⅰ)将日利润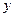 (元)表示为日产量
(元)表示为日产量 (件)的函数;
(件)的函数;
(Ⅱ)该厂的日产 量为多少件时,日利润最大?
量为多少件时,日利润最大?
( )
)
若对满足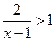 的任意实数
的任意实数 ,使得不等式
,使得不等式 恒成立,
恒成立,
求实数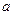 的取值范围.
的取值范围.
已知a为实数,函数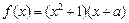
(1)若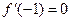 ,求函数
,求函数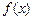 在定义域上的极大值和极小值;
在定义域上的极大值和极小值;
(2)若函数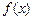 的图象上有与x轴平行的切线,求a的取值范围。
的图象上有与x轴平行的切线,求a的取值范围。