(本小题满分12分)
已知函数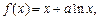 其中a为常数,且
其中a为常数,且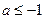 .
.
(Ⅰ)当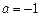 时,求
时,求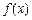 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域;
(Ⅱ)若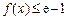 对任意
对任意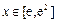 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知椭圆C: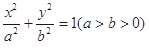 .
.
(1)若椭圆的长轴长为4,离心率为 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围
设函数 在
在 及
及 时取得极值.
时取得极值.
(1)求 、b的值;
、b的值;
(2)若对于任意的 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.
在直接坐标系xOy中,直线L的方程为x-y+4=0,曲线C的参数方程为 .
.
(1)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线L的位置关系;
),判断点P与直线L的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
设全集 ,已知集合
,已知集合 ,
,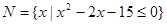 .
.
(1)求 ;
;
(2)记集合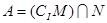 ,已知集合
,已知集合 ,若
,若 ,求实数a的取值范围.
,求实数a的取值范围.
已知命题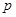 :方程
:方程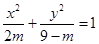 表示焦点在
表示焦点在 轴上的椭圆;命题
轴上的椭圆;命题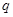 :双曲线
:双曲线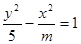 的离心率
的离心率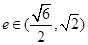 .若
.若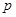 或
或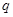 为真命题,
为真命题,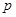 且
且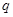 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.