(11·贵港)
如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°, CE=2BE,试判断△CDE的形状,并说明理由.
CE=2BE,试判断△CDE的形状,并说明理由.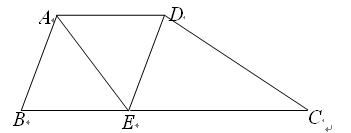
已知:关于 的二次函数y=px2-(3p+2)x+2p+2(p>0)
的二次函数y=px2-(3p+2)x+2p+2(p>0)
(1)求证:无论p为何值时,此函数图象与x轴总有两个交点;
(2)设这两个交点坐标分别为(x1,0),(x2,0)(其中x1<x2)且S=x2-2x1,求S关于P的函数解析式
甲口袋中装有两个相同的小球,它们分别写有1和2;乙口袋中装有三个相同的小球,它们分别写有3.4和5;丙口袋中装有两个相同的小球,它们分别写有6和7.从这3个口袋中各随机地取出1个小球.请你用画树状图的方法求:
(1)取出的3个小球上恰好有两个偶数的概率是多少?
(2)取出的3个小球上全是奇数的概率是多少?
已知抛物线y=ax2+bx+c经过(-1,0),(0,-3),(2,-3)三点,求这条抛物线的解析式,并指出对称轴和顶点坐标.
(1)计算: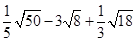 .
.
(2)用配方法解方程:x2-2x-1=0
如图,在平面直角坐标系xoy中,以点M(1,-1)为圆心,以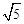 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数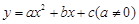 的图象经过点A、B、C,顶点为E.
的图象经过点A、B、C,顶点为E.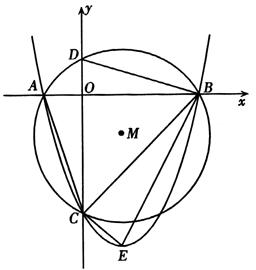
(1)求此二次函数的表达式;
(2)设∠DBC=a,∠CBE=b,求sin(a-b)的值;
(3)坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.