(本小题满分8分。其中(1)小题4分,(2)小题4分)
如图3:在正方形网格上有一个△ABC.
(1)作出△ABC关于直线MN的对称图形;
(2)若网格上最小正方形的边长为1,求△ABC的面积.
为迎接6月5日的“世界环境日”,某校团委开展“光盘行动”,倡议学生遏制浪费粮食行为.该校七年级(1)、(2)、(3)三个班共128人参加了活动.其中七(3)班48人参加,七(1)班参加的人数比七(2)班多10人,请问七(1)班和七(2)班各有多少人参加“光盘行动”?
如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题: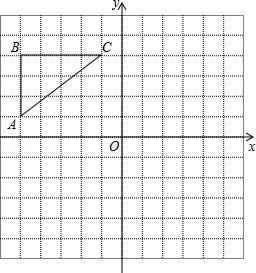
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)点C1的坐标是 ;点C2的坐标是 ;过C、C1、C2三点的圆的圆弧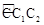 的长是 (保留π).
的长是 (保留π).
据悉,2013年财政部核定海南省发行的60亿地方政府“债券资金”,全部用于交通等重大项目建设.以下是60亿“债券资金”分配统计图:

(1)请将条形统计图补充完整;
(2)在扇形统计图中,a= ,b= (都精确到0.1);
(3)在扇形统计图中,“教育文化”对应的扇形圆心角的度数为 °(精确到°1)
计算:(1)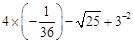 ;
;
(2)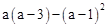 .
.
在平面直角坐标系中,已知M1(3,2),N1(5,﹣1),线段M1N1平移至线段MN处(注:M1与M,N1与N分别为对应点).
(1)若M(﹣2,5),请直接写出N点坐标.
(2)在(1)问的条件下,点N在抛物线 上,求该抛物线对应的函数解析式.
上,求该抛物线对应的函数解析式.
(3)在(2)问条件下,若抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC:OF=2: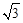 ,求m的值.
,求m的值.
(4)在(3)问条件下,动点P从B点出发,沿x轴正方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的 ,求此时BP的长度.
,求此时BP的长度.