(本小题满分12分)
某商店预备在一个月内分批购入每张价值为20元的书桌共36台,每批都购入x台(x是正整数),且每批均需付运费4元,储存购入的书桌一个月所付的保管费与每批购入书桌的总价值(不含运费)成正比,若每批购入4台,则该月需用去运费和保管费共52元,现在全月只有48元资金可以用于支付运费和保管费.
(1)求该月需用去的运费和保管费的总费用
(2)能否恰当地安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
 已知椭圆
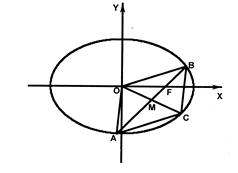
已知椭圆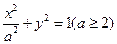 ,直线
,直线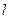 与椭圆交于
与椭圆交于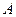 、
、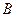 两点,
两点,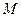 是线段
是线段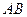 的中点,连接
的中点,连接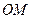 并延长交椭圆于点
并延长交椭圆于点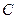 .
. 设直线
设直线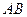 与直线
与直线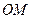 的斜率分别为
的斜率分别为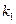 、
、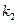 ,且
,且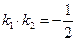 ,求椭圆的离心率.若直线
,求椭圆的离心率.若直线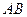 经过椭圆的右焦点
经过椭圆的右焦点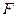 ,且四边形
,且四边形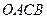 是平行四边形,求直线
是平行四边形,求直线 斜率的取值范围.
斜率的取值范围.

(本小题满分12分) 已知函数
已知函数 ,
, ,
,
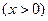 的最小值恰好是方程
的最小值恰好是方程 的三个根,其中
的三个根,其中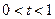 .
. (1)求证:
(1)求证: ;
; (2)设
(2)设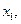
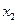 是函数
是函数 的两个极值点.若
的两个极值点.若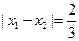 ,
, 求函数
求函数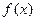 的解析式.
的解析式.

(本小题满分12分) 如图,在四棱锥P-ABCD中,
如图,在四棱锥P-ABCD中,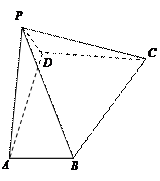
底面ABCD为直角梯形,且AB//CD,AB⊥AD,AD=CD=2AB=2.
侧面 为正三角形,且平面PAD⊥平面ABCD.网
为正三角形,且平面PAD⊥平面ABCD.网
(1)若M为PC上一动点,则M在何位置时,PC⊥平面MDB?并加已证明;(2)若G为 的重心,求二面角G-BD-C大小.
的重心,求二面角G-BD-C大小.
 某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是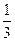 ,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试. (1)求该学生恰好经过4次测试考上大学的概率;
(1)求该学生恰好经过4次测试考上大学的概率; (2)求该学生考上大学的概率.
(2)求该学生考上大学的概率.

(本小题满分14分)已知函数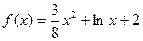 ,
,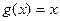 .
.
(Ⅰ)求函数 的极值点;(Ⅱ)若函数
的极值点;(Ⅱ)若函数 在
在 上有零点,求
上有零点,求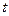 的最大值;(Ⅲ)证明:当
的最大值;(Ⅲ)证明:当 时,有
时,有 成立;若
成立;若 (
(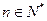 ),试问数列
),试问数列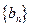 中是否存在
中是否存在 ?若存在,求出所有相等的两项;若不存在,请说明理由.(
?若存在,求出所有相等的两项;若不存在,请说明理由.(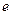 为自然对数的底数)
为自然对数的底数)